挑戦する
サモデキン教授は、キューブエッジの一致を使用して、一致からキューブの3次元モデルを作成することにしました。 各立方体のエッジの長さは、1マッチに等しくなります。
3つのサイコロのモデルを作成するために、彼は28試合を使用しました。
N個のキューブのモデルを構築するためにSamodelkinが必要とする一致の最小数はどれくらいですか?
問題のすべての数値は2・10 9を超えません。
技術的条件
入力データ
1つの数値Nはキューブの数です。
インプリント
1つの数字は一致の数です。
動的プログラミングを使用してこの問題を解決しましたが、他の方法で解決することもできますし、最後に導出する1つの式だけでも解決できます。
「ただし、列挙された問題と他のいくつかの問題の中で、1つの優れた特性を持つ問題のクラスを区別できます。いくつかのサブ問題(たとえば、nが小さい場合)の解決策があるため、ほとんど列挙せずに元の問題の解決策を見つけることができます。」- 動的プログラミングによって解決される問題のクラス
そして、私たちの目標は、動的プログラミングタスクの説明に従ってソリューションを達成することです。この場合、現在のパラメーターのソリューションは、以前のパラメーターのソリューションに基づいています。
解決策
このタスクを3つの段階に分けました。
- 1Dケースの問題を解決し、その中に1辺が一致する正方形を使用して式を導出します
- 2Dケースの問題を解決し、その中に1辺が一致する正方形を使用して、式を導出します
- 1Dおよび2Dケースのパターンを見つけ、それらに基づいて3Dケースの問題を解決し、3Dケースの式を導き出す
- n次元のケースに関する考察
1D
そして、問題の条件を確立します。
1辺が1マッチのN個の正方形のラインを構築するために必要な最小一致数を見つける必要があります

DP配列を使用して結果を保存します。
ここで、図を見て、i-1の場合のソリューションに追加する必要がある数字をこの配列に入力します。
| N: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| DP: | 0 | 4 | 3 | 3 | 3 | 3 | 3 | 3 |
そして、Nの答えは、 0からNまでのDP配列の要素の合計であり、すぐにパターンを見ることができます-DP [1]:= 4 、 DP [> 1]:= 3
そして、式を導出します(Nは常に1以上、つまり自然です):
結果(N) := SUM(DP 1- > DP N )= 4+(N-1)* 3
2D
チャレンジ:
1辺に1辺の正方形を構築するために必要な最小一致数を見つける必要があります。 2次元で構築できます。
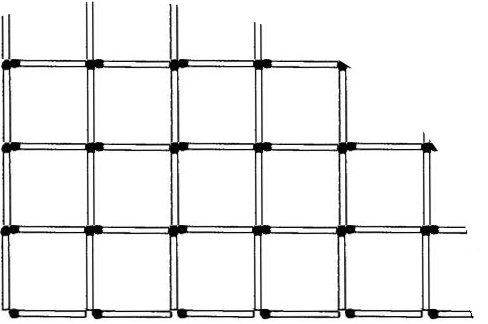
2Dでは、新しい問題があります。Ax Bは、一致の数を最小限にするためにどのサイズの平面を努力する必要がありますか? そして多くの人が推測しているように、これはもちろん正方形です。 しかし、すべてがそれほど単純ではないため、このアイデアを単純化する必要があります。
上の図を見ると、新しい正方形の最も好ましい位置は、より多くの隣人がいる場所であり、最良の場合、2つの隣人になることがわかります。
つまり、最適なケースは次のようにビルドすることです。
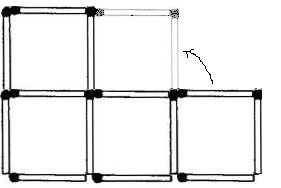
次のキューブを自分の手で作成すれば、どこに構築するかを簡単に言うことができますが、どのようにそれをコンピューターに伝えることができますか?
一枚の紙を取り、正方形から特定の平面を構築し、エッジの数を最小化すると、構築方法に気付きます。
最初は1x1-1の正方形でしたが、2x1-2の正方形に拡張してから、
2x2-3、そして4つの正方形
3x2-5と6の正方形
3x3-7.8.9平方
よく見てパターンを確認してください:エッジの数を最小化するためのA x B平面があります。次に平面を構築するのは(A + 1)x Bで、次に(A + 1)x(B + 1)で、後者は正方形です。 1 x 1から構築を開始
DP配列のテーブルを書きましょう:
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 大きさ | 1×1 | 2×1 | 2×2 | 2×2 | 3×2 | 3×2 | 3×3 | 3×3 | 3×3 |
| DP | 4 | 3 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
テーブルを分析します。
DP [1] = 4の場合
さらに、新しい行を追加するとき、3つの一致を使用して新しい正方形を作成し、行の最後まで2つの一致で正方形を終了します。 それでも思い出さないものではない 1Dの場合を思い出してください-最初の正方形は4マッチ、残りは3で、この場合は同じ追加行ですが、最初の正方形は3マッチ、残りは2マッチです。
| 2Dの場合はN | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1Dの場合はN | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 2 | 3 |
| 大きさ | 1×1 | 2×1 | 2×2 | 2×2 | 3×2 | 3×2 | 3×3 | 3×3 | 3×3 |
| DP | 4 | 3 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
解法アルゴリズム:
DP[1]=4
A=1
B=1 // A x B
1 N A B DP 1D A B :
j=1 // DPfor1D, DPfor1D={3,2,2,2,2,2,2,2,...}
for i = 2 -> N
begin
if A*B<i
then begin
(A<B)?A++:B++
j=1
end
DP[i]:= DP[i-1]+DPfor1D[j]
j++
end
または:
Result:= 4
newN:= 1
A:= 2
B:= 1
while newN <= N
begin
Result:= Result + 1D(min(A,B)) // 1D(N):=3+(N-1)*2 N >= 1, 0
(A<B)?A++:B++
newN=A*B
end
(A>B)?A--:B--
Result:= Result+ 1D(NA*B)
そして式:
結果(N) := 4 + 3 *(1を除いた数Nまでの完全な正方形の数+完全な正方形の前にある追加の数)+ 2 *(その他すべて)
N SQRT := int(sqrt(N))-1
N ADD := N SQRT + 1(N <= N SQRT *(N SQRT +1)の場合)
結果(N) := 4 + 3 *(N SQRT + N ADD )+ 2 *(NN SQRT -N ADD )
3D
それで、3Dケースに到達しました
3次元の場合、構築の一致数を最小限に抑えるために、キューブは大きなキューブの構築を目的とする必要がありますが、中間の場合は次のようになります。
A x B x C->(A + 1)x B x C->(A + 1)x(B + 1)x C->(A + 1)x(B + 1)x(C + 1)
ソリューションアルゴリズムは2Dの場合と同じですが、いくつかの新しい機能が与えられます。
1D(N):= 5+(N-1)* 3
2D(N):=上記のサブセクションで指定されたアルゴリズム、ただし調整あり-2D(1):= 8
3D(N):=上記の2Dの場合のアルゴリズム、ただし3次元を考慮-3D(1):= 12、座標が増加すると、結果を次のように変更します:結果:=結果+ 2D(A * B * C /最大(A、B、C))、つまり 新しいボックスのパラメーターを変更して、追加されたプレーンのサイズから2Dを取得する必要があります
そして3Dの式
数式は2Dの数式と同じ部分で構成されますが、完全な正方形だけでなく完全なキューブも考慮します
結果(N) := 12 + 8 *(3 * N フルキューブ +(Nに応じて0または1または2))+ 5 *(2 * N フルスクエア +(Nに応じて0または1))+ 3 * N レスト
しかし、残念なことに、この公式は完全に正しいわけではなく、いくつかの例外や修正を熟考するためにより多くの精神的な努力が必要です。
n次元のケースに関する考察
前のセクションでは、立方体/正方形の一致の最小化が依存するものを調べ、これに基づいて、任意の測定のアルゴリズムを作成できます。
元のN次元の正方形が何個のマッチで構成されているかを検討し、新しい要素の構築を完了するのに必要なマッチの数を計算する必要があります。
オブジェクトの次元をキャプチャするためのアルゴリズムを推定しました-反復ごとに、最小次元が1ずつ増加します。
また、オブジェクトのサイズを変更するときは、追加されたプレーンのサイズから(N-1)番目の測定値の関数の値を追加する必要があることに気付きました。
数式を作成するときは、N度、N-1、N-2などの数字の数を考慮する必要があります。 +機能を考慮する
参照資料
E-olimp-ウクライナの教育機関の才能のある若者向けの遠隔プログラミングオリンピックの組織的および方法論的サポートのためのインターネットポータル。
渡そうとするポータル上のタスク -登録が必要です
動的プログラミングの記事