多くのolympiadプログラミングの問題では、再帰的検索または網羅的検索を使用するソリューションでは、非常に多くの操作が必要です。 たとえば、徹底的な検索によってこのような問題を解決しようとすると、実行時間が過剰になります。
ただし、網羅的な問題と他のいくつかの問題の中で、1つの優れた特性を持つ問題のクラスを区別できます:いくつかの副問題(たとえば、より小さな数n )に対する解決策があるため、ほとんど列挙せずに元の問題の解決策を見つけることができます。
このような問題は、動的計画法によって解決され、動的計画法自体は、問題をサブタスクに還元することを意味します。
シーケンス
シーケンスの古典的な問題は次のとおりです。
フィボナッチ数列F nは次の式で与えられます: F 1 = 1、 F 2 = 1、
n > 1の場合、 F n = F n -1 + F n -2 。番号nで F nを見つける必要があります。
論理的かつ効率的と思われる1つのソリューションは、再帰ベースのソリューションです。
int F(int n){
if(n <2)1を返します。
それ以外の場合は、F(n-1)+ F(n-2)を返します。
}
このような関数を使用して、「最後から」問題を解決します。既知の値に達するまで、段階的にnを減らしていきます。
しかし、ご覧のとおり、このような一見単純なプログラムは、 n = 40ですでにかなり長い間機能しています。 これは、同じ中間データが数回計算されるという事実に起因します-フィボナッチ数が増加するのと同じ速度で操作の数が増加する-指数関数的に。
この状況から抜け出す1つの方法は、すでに見つかった中間結果を再利用する目的で保存することです。
int F(int n){
if(A [n]!= -1)return A [n];
if(n <2)1を返します。
その他{
A [n] = F(n-1)+ F(n-2);
return A [n];
}
}
与えられた解決策は正しく効果的です。 ただし、このタスクには、より単純なソリューションが適用できます。
F [0] = 1; F [1] = 1; for(i = 2; i <n; i ++)F [i] = F [i-1] + F [i-2];
このようなソリューションは、「最初から」ソリューションと呼ばれます。最初に既知の値を入力し、次に最初の未知の値( F 3 )を見つけ、次に次の値を見つけて、正しい値に到達するまで続きます。
ダイナミックプログラミングの古典的なソリューションです。最初にすべてのサブタスクを解決し( i < nのすべてのF iを見つけました)、サブタスクの解決策を知って、答えを見つけました( F n = F n -1 + F n -2 、 F n -1およびF n -2がすでに見つかっています)。
一次元動的プログラミング
動的プログラミングの本質をよりよく理解するために、まずタスクとサブタスクの概念をより正式に定義します。
最初の問題は、初期データn 1 、 n 2 、...、 n kである数Tを見つけることです。 つまり、関数T ( n 1 、 n 2 、...、 n k )について話すことができ、その値が必要な答えです。 次に、タスクをサブ問題と見なします
T ( i 1 、 i 2 、...、 i k )for i 1 < n 1 、 i 2 < n 2 、...、 i k < n k 。
さらに、それぞれk = 1、 k = 2、 k > 2の場合の1次元、2次元、および多次元の動的プログラミングについて説明します。
1次元動的プログラミングの次のタスクは、さまざまなバリエーションにあります。
問題1. 2つの連続したユニットが発生しないゼロのシーケンスと長さnのユニットの数を計算します。
n <32の場合、完全な列挙には数秒かかり、 n = 64の場合、原則として完全な列挙は実行できません。 動的計画法により問題を解決するために、元の問題をサブタスクに減らします。
n = 1、 n = 2の場合、答えは明らかです。 K n -1がすでに見つかっていると仮定します。Kn -2は、長さn -1およびn -2のそのようなシーケンスの数です。
長さnのシーケンスがどのようになるかを見てみましょう。 最後の文字が0の場合、最初のn -1は長さの規則的なシーケンスです
n -1(0で終わる0で終わるか、1で終わるかは関係ありません)。 このようなシーケンスはK n -1のみです。 最後の文字が1である場合、最後から2番目の文字は0に等しくなければなりません(そうでなければ、2つの単位が連続します)。
n -2文字-長さn -2の通常のシーケンス。そのようなシーケンスの数はK n -2です。

したがって、 n > 2の場合 、 K 1 = 2、 K 2 = 3、 K n = K n -1 + K n -2です。つまり、この問題は実際にはフィボナッチ数を見つけることになります。
二次元動的計画法
古典的な2次元の動的プログラミングの問題は、長方形のフィールドでのルートの問題です。
さまざまな定式化では、ルートの数を計算するか、ある意味で最適なルートを見つける必要があります。
そのような問題のいくつかの定式化を次に示します。
問題2.サイズがn * mの長方形のフィールドを与えます。 1セル分右または下にステップを実行できます。 左上のセルから右下のセルまでの道のりの数を数えます。
タスク3.セルのサイズがn * mの長方形フィールドを指定します。 1セル分右、下、または斜め右下にステップを実行できます。 各セルには特定の自然数が含まれています。 左上のセルから右下に移動する必要があります。 ルートの重みは、訪問したすべてのセルの数値の合計として計算されます。 重みが最小のルートを見つける必要があります。
このようなすべてのタスクについて、個々のルートが同じセルに沿って複数回通過できないことが特徴です。
タスク2をさらに詳しく見てみましょう。座標( i 、 j )を持つセルには、上または左からのみ、つまり座標( i -1、 j )および( i 、 j -1)を持つセルからのみアクセスできます:

したがって、セル( i 、 j )の場合、ルートA [i] [j]の数は次のようになります。
A [i-1] [j] + A [i] [j-1]、つまり、タスクは2つのサブタスクに要約されます。 この実装では、2つのパラメーター-iとj-が使用されるため、この問題に適用されるように、2次元の動的プログラミングについて話します。
これで、配列Aの行(または列)を順番に調べて、上記の式を使用して現在のセルのルートの数を見つけることができます。 以前は、番号1はA [0] [0]に配置する必要があります。
問題3では、座標を持つセルから座標( i 、 j )を持つセルに入ることができます
( i -1、j)、( i 、 j -1)および( i -1、 j -1)。 これら3つのセルのそれぞれについて、すでに最小の重みのルートを見つけており、W [i-1] [j]、W [i] [j-1]に重みを配置したとします。
W [i-1] [j-1]。 ( i 、 j )の最小重みを見つけるには、重みの最小値W [i-1] [j]、W [i] [j-1]、W [i-1] [j-1]を選択して追加する必要があります現在のセルに記録されている番号:
W [i] [j] = min(W [i – 1] [j]、W [i] [j-1]、W [i-1] [j-1])+ A [i] [j] ;
このタスクは、最小重量だけでなく、ルート自体も見つける必要があるという事実によって複雑になります。 したがって、別の配列では、各セルについて、どちらの側に入れる必要があるかを追加で書き留めます。
次の図は、ソースデータの例とアルゴリズムのステップの1つを示しています。
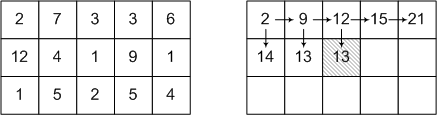
正確に1つの矢印が、すでに通過したセルのそれぞれにつながります。 この矢印は、セルに記録された最小重量を取得するためにこのセルに入る必要がある側を示しています。
アレイ全体を通過した後、反対方向の矢印に従って最後のセルからルート自体をトレースする必要があります。
サブシーケンスタスク
サブシーケンスが増加する問題を検討してください。
問題4.整数のシーケンスが与えられます。 最長の厳密に増加するサブシーケンスを見つける必要があります。
最初から問題の解決を始めましょう-このシーケンスの最初のメンバーから始めて、答えを探します。 各数値iについて、位置iの要素で終わる最大の増加サブシーケンスを検索します。 初期シーケンスを配列Aに保存します。配列Lには、現在の要素で終わる最大サブシーケンスの長さを記録します。 1 <= i <= k -1のすべてのL [i]を見つけたとしましょう。次のようにL [k]を見つけることができます。 1 <= i < k -1のすべての要素A [i]を調べます。
A [i] <A [k]の場合、 k番目の要素は、A [i]で終わるサブシーケンスの継続となります。 得られたサブシーケンスの長さは、L [i]より1大きくなります。 L [k]を見つけるには、1からk-1までのすべてのiを整理する必要があります。
L [k] = max(L [i])+1。ここで、A [i] <A [k]および
1 <= i < k 。
ここでは、空のセットの最大値は0に等しいと見なされます。この場合、現在の要素は選択されたシーケンス内の唯一の要素になり、前の要素の1つに続くことはありません。 配列Lを埋めた後、最大の増加サブシーケンスの長さは最大要素Lに等しくなります。
サブシーケンス自体を復元するために、各要素が、以前に選択された要素の番号を、たとえば配列Nに保存することもできます。
シーケンス2、8、5、9、12、6の例を使用して、この問題の解決策を検討します。2までの要素はないため、最大サブシーケンスには要素が1つだけ(L [1] = 1)、その前に1つはありません-N [1] =0。さらに、
2 <8であるため、8は前の要素とのシーケンスの継続となります。 次に、L [2] = 2、N [2] = 1。
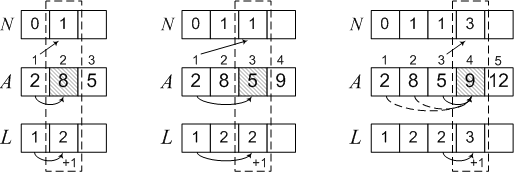
A [3] = 5未満は要素A [1] = 2のみであるため、5は1つのサブシーケンス(2を含むサブシーケンス)のみの継続となります。
L [3] = L [1] + 1 = 2、N [3] =1。2は1の位置にあるため、同様に、アルゴリズムのさらに3つのステップを実行し、最終結果を取得します。
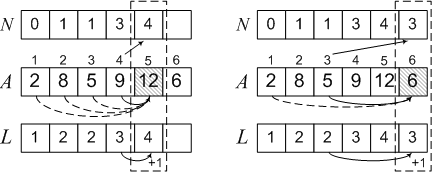
ここで、配列Lの最大要素を選択し、配列Nからサブシーケンス自体2、5、9、12を復元します。
もう1つの古典的な動的プログラミングの問題は、回文の問題です。
タスク5.ラテンアルファベットの大文字の文字列を指定します。 最大のパリンドロームの長さを見つける必要があります。これは、この行からいくつかの文字を削除することで取得できます。
この行をSで表し、その文字をS [i]、1 <= i <= nで表します。 この文字列のi番目からj番目の文字までの可能な部分文字列を検討し、それらをS ( i 、 j )で示します。 部分文字列の最大回文の長さは、正方配列Lに書き込まれます。L[i] [j]は、部分文字列S ( i 、 j )から取得できる最大回文の長さです。
最も単純な部分文字列で問題の解決を始めましょう。 1文字の文字列(つまり、フォームS ( i 、 i )の部分文字列)の場合、答えは明白です-削除する必要はありません。そのような文字列は回文です。 2文字の文字列S ( i 、 i + 1)には、2つのオプションがあります。文字が等しい場合、回文があり、削除する必要はありません。 文字が等しくない場合は、いずれかを取り消します。
ここで、部分文字列S ( i 、 j )が与えられます。 最初の(S [i])と最後の(S [j])のサブストリング文字が一致しない場合、それらの1つを確実に消す必要があります。 次に、サブストリングS ( i 、 j -1)またはS ( i + 1、 j )を使用します。つまり、問題をサブタスクに還元します。L [i] [j] = max(L [i] [j-1] 、L [i + 1] [j])。 最初と最後の文字が等しい場合、両方を残すことができますが、問題S ( i + 1、 j -1)の解決策を知る必要があります。
L [i] [j] = L [i + 1] [j-1] + 2。
例としてABACCBA文字列を使用したソリューションを検討してください。 まず、配列の対角線を単位で埋めます。それらは1文字の部分文字列S ( i 、 i )に対応します。 次に、長さ2の部分文字列を検討し始めます。 S (4、5)を除くすべてのサブストリングでは、文字が異なるため、対応するセルに1、Lに2を書き込みます[4] [5]。
配列は、左上から右下に向かう主な対角線から始めて、斜めに配列することがわかります。 長さ3の部分文字列の場合、次の値が取得されます。部分文字列ABAでは、最初の文字と最後の文字が等しいため、
L [1] [3] = L [2] [2] + 2.残りのサブストリングでは、最初と最後の文字が異なります。
BAC:L [2] [4] =最大(L [2] [3]、L [3] [4])= 1。
ACC:L [3] [5] =最大(L [3] [4]、L [4] [5])= 2。
CCB:L [4] [6] =最大(L [4] [5]、L [5] [6])= 2。
CBA:L [5] [7] = max(L [5] [6]、L [6] [7])= 1。
さらに同様の推論を続けて、対角線の下のすべてのセルに入力し、セルL [1] [7] = 6に答えを取得します。
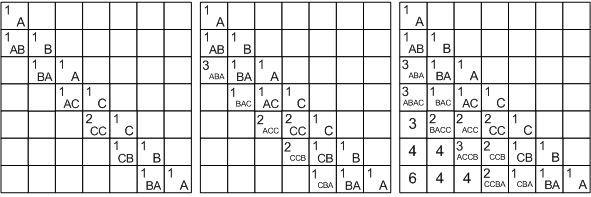
タスクで長さではなくパリンドローム自体を導出する必要がある場合は、長さ配列に加えて遷移の配列を構築する必要があります-各セルについて、実装されたケースを覚えておいてください(図では、遷移をエンコードする数値の代わりに対応する矢印が描かれています) 。