ファジィ推論システムにおけるマムダニのアルゴリズム

はじめに

たまたま、Lotfi Zadehという名前に言及して、ファジーロジックに関する記事を始めるのが慣例となっています。 そして、私も例外ではありません。 実際、この男は1965年に基礎研究「ファジィセット」を書いて科学理論全体の創始者になっただけでなく、その実用化に向けてさまざまな可能性を考え出しました。 彼は、1973年のテキスト「複雑なシステムと意思決定プロセスの分析への新しいアプローチの概要」（IEEE Transactions on Systemsで公開）でアプローチを説明しました。 注目に値するのは、1つの進取的なデンマーク企業がリリース直後に、複雑な生産プロセスの管理システムを改善するために、ここに記載されている原則を非常にうまく適用したことです。



しかし、L。ザードのすべての長所により、この理論の支持者たちも同様に重要な貢献をしました。 たとえば、英国の数学者E. Mamdani（Ebrahim Mamdani）。 1975年、彼は蒸気エンジンの制御方法として提案されたアルゴリズムを開発しました。 ファジィ推論に基づいて彼が提案したアルゴリズムは、過度に大量の計算を回避することを可能にし、専門家に高く評価されました。 このアルゴリズムは現在、ファジーモデリングの問題で最も実用的なアプリケーションになっています。

キー定義

アルゴリズムに慣れる前に、次の定義を簡単に理解することが重要です。



ファジー変数は、<α、 X 、 Α >という形式のタプルです。ここで、

αはファジー変数の名前です。

Xはその定義のドメインです。

Aは、ユニバースX上のファジーセットです。



例：ファジー変数<"Heavy body armor"、{ x | 0 kg < x <35 kg}、 B = { x 、μ（ x ）}>は、軍用ボディアーマーの質量を特徴づけます。 質量が16 kgを超える場合は、重量が大きいと見なされます（図1）。







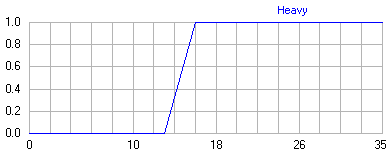
図 1.ファジーセットBのメンバーシップ関数μ（ x ）のグラフ



言語変数はタプル<β、 T、X、G、M >です。ここで：

βは言語変数の名前です。

Tはその意味（用語）のセットです。

Xはファジー変数の宇宙です。

Gは、新しい用語を形成するための構文手順です。

Mは、特定の言語変数の各用語に対してファジーセットを形成するセマンティックプロシージャです。



例：ボディアーマーの重量の主観的な評価があるとします。 たとえば、このような弾薬を直接扱う軍人（専門家として行動する）から入手できます。 この推定は、次の言語変数<β、 T、X、G、M >（図2）を使用して形式化できます。ここで、

β-ボディアーマー。

T- {「ライトボディアーマー（ライト）」、「ミディアムウェイトボディーアーマー（ミディアム）」、「ヘビーボディーアーマー（ヘビー）」};

X = [0; 35];

G-論理接続詞と修飾子を使用した新しい用語の形成手順。 たとえば、「非常に重いボディアーマー」。

MはユニバースのタスクプロシージャX = [0; 35]言語変数の値、すなわち セットTからの用語







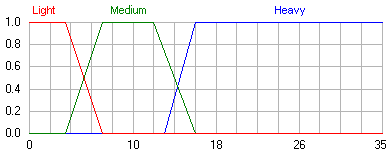
図 2.言語変数「防弾チョッキ」の値のメンバーシップ関数のグラフ



ファジーステートメントは、 「βISα」という形式のステートメントです。ここで、

βは言語変数です。

αはこの変数の項の1つです。



例： 「IS軽量ボディアーマー。」 ここで、「防弾チョッキ」は言語変数であり、その「軽い」意味です。



簡単に言えば、 ファジー製品のルール （以下、単にルール）は、「IF ... THEN ...」という形式の古典的なルールであり、ファジーステートメントが条件と結論として使用されます。 そのようなルールは、次の形式で記述されます。



IF（β1 ISα1）AND（β2 ISα2）THEN（β3 ISα3）。



「AND」に加えて、論理接続詞「OR」も使用されます。 しかし、彼らは通常、そのようなルールをいくつかのより単純なルール（「OR」なし）に分割することで、そのようなレコードを回避しようとします。 また、ルールの条件にある各ファジー文は、 サブ条件と呼ばれます。 同様に、結論の各文は副次句と呼ばれます。



例：次の例は、定義をキャプチャするのに役立ちます。



1）IF（重防弾チョッキ）THEN（退役軍人）;

2）IF（夫は冷静）AND（高給）THEN（満足した妻）。



それだけです この最小値は、アルゴリズムの原理を理解するのに十分です。

Mamdaniアルゴリズム

このアルゴリズムは、いくつかの連続した段階を記述します（図3）。 同時に、後続の各ステージは、前のステップで取得した値を入力として受け取ります。







図 3.ファジー推論プロセスのアクティビティ図



このアルゴリズムは、「ブラックボックス」の原理で機能する点で注目に値します。 入力は定量的な値を受け取り、出力は同じです。 中間段階では、ファジーロジックの装置とファジーセットの理論が使用されます。 これは、ファジーシステムを使用することの優雅さです。 通常の数値データを操作できますが、同時にファジー推論システムが提供する柔軟な機能を使用します。



アルゴリズムを実装するために、オブジェクト指向のアプローチが使用されました。 ソースコードはJavaプログラミング言語で記述されています。 図（図4）は、最も重要な関係と、アルゴリズムに関係するクラス間の関係を示しています。







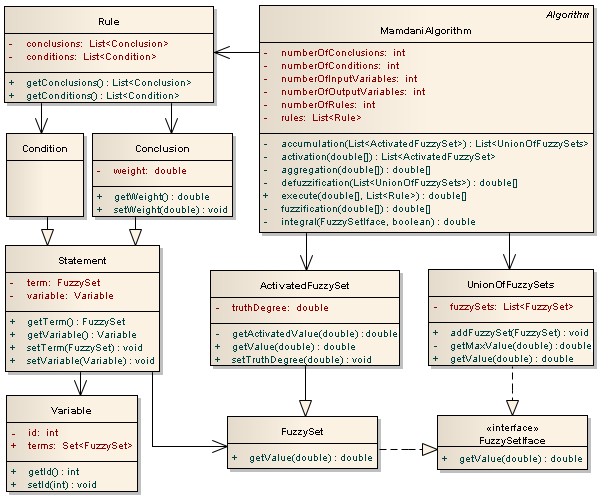
図 4. Mamdaniアルゴリズムの実装のクラス図



ルール（ルール）は条件（条件）と結論（結論）で構成され、これらはファジーステートメント（ステートメント）です。 ファジーステートメントには、言語変数（変数）と、ファジーセットで表される用語（FuzzySet）が含まれます。 メンバーシップ関数はファジーセットで定義され、その値はgetValue（）メソッドを使用して取得できます。 これは、FuzzySetIfaceインターフェイスで定義されているメソッドです。 アルゴリズムを実行する場合、「有効化」ファジーセット（ActivatedFuzzySet）を使用する必要があります。これは、何らかの方法でファジーセット（FuzzySet）のメンバーシップ関数を再定義します。 このアルゴリズムは、ファジーセットの和集合（UnionOfFuzzySets）も使用します。 ユニオンもファジーセットであるため、メンバーシップ関数（FuzzySetIfaceで定義）があります。



Mamdaniアルゴリズム（MamdaniAlgorithm）は、すべてのステージを含み（図3）、ルールベース（リスト<ルール>）を入力として使用します。 このアルゴリズムには、「アクティブ化された」ファジーセット（ActivatedFuzzySets）とそれらの関連付け（UnionOfFuzzySets）の使用も含まれます。



したがって、ファジー推論の段階は連続して実行されます。 そして、前のステップで取得したすべての値は、次のステップで使用できます。



1.ルールベースの形成

ルールベースは、各副次句が特定の重み係数に関連付けられている一連のルールです。



ルールベースには次の形式を使用できます（たとえば、さまざまな構造のルールが使用されます）。



RULE_1：「Condition_1」の場合、「Conclusion_1」（ F ₁ ）および「Conclusion_2」（ F ₂ ）。

RULE_2：「Condition_2」および「Condition_3」の場合、「Conclusion_3」（ F ₃ ）。

...

RULE_n：「Condition_k」の場合、「Conclusion_（q-1）」（ F _q-1 ）および「Conclusion_q」（ F _q ）。



ここで、 F _i-重み付け係数。結果のサブコントラクトの真理に対する信頼度を示します（ i = 1 .. q ）。 デフォルトでは、重み係数は1と見なされます。条件に存在する言語変数はinputと呼ばれ、結論ではoutputと呼ばれます 。



指定：

nはファジー生成規則の数（numberOfRules）です。

m-入力変数の数（numberOfInputVariables）。

s-出力変数の数（numberOfOutputVariables）。

kは、ルールベースのサブ条件の総数（numberOfConditions）です。

qは、ルールベース内のサブ接続の総数（numberOfConclusions）です。



注：これらの記号は、以降の手順で使用されます。 括弧内は、ソースコード内の対応する変数の名前です。



2.入力変数のファジー化

この手順は、あいまいさの軽減と呼ばれます。 形成されたルールベースと入力データ配列A = {a ₁ 、...、a _m }が入力されます。 この配列には、すべての入力変数の値が含まれます。 このステップの目的は、ルールベースからすべてのサブ条件の真理値を取得することです。 これは次のように発生します。各副条件について、値b _i =μ（ a _i ）が見つかります。 したがって、値のセットb _i （ i = 1 .. k ）が取得されます。



実装：

private double [] fuzzification( double [] inputData) {

int i = 0;

double [] b = new double [numberOfConditions];

for (Rule rule : rules) {

for (Condition condition : rule.getConditions()) {

int j = condition.getVariable().getId();

FuzzySet term = condition.getTerm();

b[i] = term.getValue(inputData[j]);

i++;

}

}

return b;

}







注：入力データ配列は、配列のi番目の要素がi番目の入力変数に対応するように形成されます（変数番号は整数フィールド「id」に格納されます）。



3.前提条件の集約

上記のように、ルール条件は複合、つまり 論理演算「AND」を使用して相互接続されたサブ条件を含めます。 この段階の目的は、ファジー推論システムの各ルールの条件の真実度を判断することです。 簡単に言えば、各条件について、そのすべてのサブ条件の真理の最小値を見つけます。 正式には、次のようになります。



c _j = min { b _i }。



どこで：

j = 1 .. n ;

iは、 j番目の入力変数が含まれるサブ条件の数のセットの数です。



実装：

private double [] aggregation( double [] b) {

int i = 0;

int j = 0;

double [] c = new double [numberOfInputVariables];

for (Rule rule : rules) {

double truthOfConditions = 1.0;

for (Condition condition : rule.getConditions()) {

truthOfConditions = Math .min(truthOfConditions, b[i]);

i++;

}

c[j] = truthOfConditions;

j++;

}

return c;

}







4.外注の有効化

この段階では、条件から下請けへの移行があります。 各サブクルージョンについて、真の度合いはd _i = c _i * F _iであり、 i = 1 .. qです。 次に、各i番目のサブクルージョンについて、セットD _iが新しいメンバーシップ関数に関連付けられます。 その値は、少なくともd _iと副次項の項メンバーシップ関数の値から決定されます。 このメソッドはmin-activationと呼ばれ、正式には次のように記述されます。



μ ^' _i （ x ）= min { d _i 、μi（ x ）}。



どこで：

μ ^' _i （ x ）-「アクティブ化された」メンバーシップ関数。

μi（ x ）-期間メンバーシップ関数。

d _i - i番目のサブコネクションの真実度。



したがって、この段階の目標は、ルールベース（ i = 1 .. q ）の各副次句について、「アクティブな」ファジーセットD _iのセットを取得することです。



実装：

private List <ActivatedFuzzySet> activation( double [] c) {

int i = 0;

List <ActivatedFuzzySet> activatedFuzzySets = new ArrayList <ActivatedFuzzySet>();

double [] d = new double [numberOfConclusions];

for (Rule rule : rules) {

for (Conclusion conclusion : rule.getConclusions()) {

d[i] = c[i]*conclusion.getWeight();

ActivatedFuzzySet activatedFuzzySet = (ActivatedFuzzySet) conclusion.getTerm();

activatedFuzzySet.setTruthDegree(d[i]);

activatedFuzzySets.add(activatedFuzzySet);

i++;

}

}

return activatedFuzzySets;

}







private double getActivatedValue( double x) {

return Math .min(super.getValue(x), truthDegree);

}







5.結論の蓄積

このステージの目的は、各出力変数のファジーセット（またはその組み合わせ）を取得することです。 次のように実行されます_。i番目の出力変数は、集合E _i =∪D _jの和集合に関連付けられます。 jは、 i番目の出力変数（ i = 1 .. s ）が含まれるサブコネクションの数です。 2つのファジーセットの和集合は、次のメンバーシップ関数を持つ3番目のファジーセットです。



μ ^' _i （ x ）= max {μ1（ x ）、μ2（ x ）}、ここでμ1（ x ）、μ2（ x ）は結合集合のメンバーシップ関数です。



実装：

private List <UnionOfFuzzySets> accumulation( List <ActivatedFuzzySet> activatedFuzzySets) {

List <UnionOfFuzzySets> unionsOfFuzzySets =

new ArrayList <UnionOfFuzzySets>(numberOfOutputVariables);

for (Rule rule : rules) {

for (Conclusion conclusion : rule.getConclusions()) {

int id = conclusion.getVariable().getId();

unionsOfFuzzySets. get (id).addFuzzySet(activatedFuzzySets. get (id));

}

}

return unionsOfFuzzySets;

}







private double getMaxValue( double x) {

double result = 0.0;

for (FuzzySet fuzzySet : fuzzySets) {

result = Math .max(result, fuzzySet.getValue(x));

}

return result;

}







6.出力変数の非ファジー化

非ファジー化の目的は、出力言語変数ごとに定量的な値（鮮明な値）を取得することです。 正式には、これは次のように発生します。 i番目の出力変数とそれに関連する集合E _i （ i = 1 .. s ）が考慮されます。 次に、非ファジー化方法を使用して、出力変数の最終的な定量値が検出されます。 このアルゴリズムの実装では、重心法が使用され、 i番目の出力変数の値は次の式で計算されます。





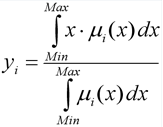
どこで：

μi（ x ）は、対応するファジーセットE _iのメンバーシップ関数です。

最小および最大は、ファジー変数の宇宙の境界です。

y _iは、ファジー化の結果です。



実装：

private double [] defuzzification( List <UnionOfFuzzySets> unionsOfFuzzySets) {

double [] y = new double [numberOfOutputVariables];

for ( int i = 0; i < numberOfOutputVariables; i++) {

double i1 = integral(unionsOfFuzzySets. get (i), true );

double i2 = integral(unionsOfFuzzySets. get (i), false );

y[i] = i1 / i2;

}

return y;

}

おわりに

Mamdaniのアルゴリズムと他の多くのファジー推論アルゴリズムは、Fuzzy Logic Toolbox（MatLabの拡張機能）、fuzzyTECHなどのすばらしい製品に既に実装されています。 したがって、この記事のように、このようなアルゴリズムの詳細な検討には、実用的というよりも理論的な価値があります。 ただし、アルゴリズムの基礎に関する知識と理解の強固な基盤がなければ、最大限の効果でそれを適用することはできません。

文学

説明したアルゴリズムのアプリケーションの特定の例を詳しく見たい場合は、次の文献を参照することをお勧めします。



1.レオネンコフA.V. MATLABでのファジーモデリングとfuzzyTECH / A. Leonenkov。 -サンクトペテルブルク：BHV-Petersburg、2003。-736 p。



2. Shtovba S.D. MATLAB / S. Shtovbaを使用したファジーシステムの設計。 -M：ホットライン– Telecom、2007。-288 p。