これは何ですか
フェンウィックツリーは、次のプロパティを持つ配列上のツリーであるデータ構造です。
•任意のセグメントで可逆操作Fの値を計算できます[L; R]対数時間の場合。
•O(log N)を超える要素の値を変更できます。
•O(N)メモリが必要です。
操作F
操作Fはさまざまな方法で選択できますが、ほとんどの場合、操作は間隔の合計、間隔の積、および特定の変更と制限を加えて、間隔または他の操作の最大値と最小値を見つけます。
簡単なタスク
配列の連続した要素の合計を見つける問題を考えてください。 S(L、R)-[L]から[R]までのすべての要素の合計を見つけることが必要な(L、R)の形式のクエリが多数あることを考えます。
この問題の最も簡単な解決策は、部分的な金額を見つけることです。 それらを見つけた後、これらの量を合計[i] = a [1] + a [2] ... + a [i]の配列に書き込みます。 次に、値S(L、R)=要求に必要な合計[R]-合計[L-1](個々のケースを考慮しないように、合計[0]は通常ゼロに等しいと見なされます)。
短所
しかし、このタスクのこの実装には重大な欠点があります。 そして、主なものの1つは、元の配列の1つの要素を変更すると、平均してO(N)の部分量を再計算する必要があり、これには時間がかかることです。 この問題を解決するには、フェンウィックツリーを使用できます。
メリット
この設計の主な利点は、実装の単純さと、リクエストへの応答速度(O(1)の場合)です。
このタスクのためのフェンウィックツリーアプリケーション
自然数で定義され、x&(x + 1)(&はビット単位のAND)に等しい関数G(x)を導入します。 したがって、xのバイナリ展開で最後が0(xは2で割り切れる)であれば、G(x)はxと等しくなります。 また、下位桁のxのバイナリ分解で単位のグループがある場合、関数は最後の単位を0に置き換えたxと等しくなります。これがx&(x + 1)であることを例で確認できます(図を参照)。
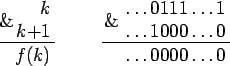
ここで、次の部分和を考慮して、t [i] = a [G [i]] + a [G [i] +1] ... + a [i]で記述します。 次に、これらの金額を見つける方法を示します。
金額計算
S(L、R)を見つけるには、S(1、L-1)およびS(1、R)を検索します。 配列tの存在下でS(L、R)を見つける関数を作成します。 この場合、左端は金額に含まれませんが、タスクで必要な場合は簡単に含めることができます(コードを参照)。
const int N=100; int t[N],a[N]; int sum(int L, int R) { int res=0; while (R >= 0) { res += t[R]; R = G( R ) - 1; } while (L >= 0) { res -= t[L]; L = G(L) - 1; } return res; }
また、各アプリケーションの関数Gにより、バイナリ表記xのユニット数が少なくとも1減少することにも注意してください。これにより、合計がO(log N)で計算されます。
要素の変更
次に、要素の変更を検討します。 要素の変化に応じて、部分量をすばやく変更する方法を学習する必要があります。 a [k]をdずつ変更します。 次に、不等式G(j)<k <jが真である配列t [j]の要素を変更する必要があります。 しかし、次のトリックが助けになります。 求められているjはすべてシーケンスk [i]に属すると述べられています(計算を参照)。

どこの下| ビット単位のORを理解します。
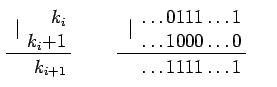
この関数は厳密に増加し、最悪の場合、数kのバイナリ展開で毎回1単位が加算されるため、時間の対数が適用されることに気付くのは簡単です。
[k]要素をdだけ変更し、同時に対応する部分和を変更する関数を作成します。
const int N=100; int t[N],a[N]; void upd(int k, int d) { a[k]+=d; while(k<N) { t[k]+=d; k=(k|(k+1)); } }
初期化
ここで、配列tの初期計算中に、ゼロで初期化できることに注意してください。 その後、N個の要素ごとにupd(i、a [i])関数を使用します。 次に、初期計算にはO(N * log N)時間かかります。これは、単純な部分和を使用した説明したアルゴリズムよりも長くなります。
ラインツリーとの比較
利点:
-すでに述べたシンプルさとスピード
-メモリはO(N)
短所:
-関数は可逆である必要があります。つまり、このツリーは最小値と最大値をカウントできません(データを犠牲にできない限り)。
おわりに
要素の合計に関するクエリに回答し、対数時間内に要素を変更することを学びました。 このアルゴリズムには多くの用途があり、操作の結果をすばやく変更して決定する必要があるすべてのタスクで役立ちます。 皆が理解し、面白いことを願っています。 ご清聴ありがとうございました。