参照ベクトル法によるデータの分類
こんにちは
この記事では、サポートベクターマシン(サポートベクターマシン、SVM)によるデータ分類の問題について説明します。 この分類には、パターン認識やスパムフィルターの作成から、ロケット排気ガス中の高温アルミニウム粒子の分布の計算まで、かなり幅広い用途があります。
最初に、元のタスクに関するいくつかの言葉。 分類タスクは、少なくとも2つの初期既知オブジェクトのどのクラスが属するかを判別することです。 通常、そのようなオブジェクトはn次元の実空間のベクトルです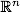 。 ベクトルの座標は、オブジェクトの個々の属性を表します。 たとえば、RGBモデルで指定された色cは、3次元空間のベクトルです: c =( red、green、blue )。
。 ベクトルの座標は、オブジェクトの個々の属性を表します。 たとえば、RGBモデルで指定された色cは、3次元空間のベクトルです: c =( red、green、blue )。
2つのクラス(「スパム/スパムではない」、「クレジットを与える/クレジットを与えない」、「赤/黒」)しかない場合、タスクはバイナリ分類と呼ばれます。 複数のクラスがある場合-マルチクラス(マルチクラス)分類。 また、各クラスのサンプルが存在する場合があります。どのクラスに属しているかが事前にわかっているオブジェクトです。 このようなタスクは教師による学習と呼ばれ、既知のデータはトレーニングサンプルと呼ばれます 。 (注:クラスが最初に定義されていない場合、クラスタリングのタスクがあります。 )
この記事で検討しているサポートベクターの方法は、教師による指導に関連しています。
したがって、分類問題の数学的定式化は次のとおりです。Xをオブジェクトの空間とします(たとえば、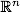 )、 Yはクラスです(たとえば、 Y = {-1,1})。 与えられたトレーニングサンプル:
)、 Yはクラスです(たとえば、 Y = {-1,1})。 与えられたトレーニングサンプル: 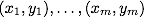 。 関数を構築する必要があります
。 関数を構築する必要があります 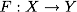 (分類子)クラスyを任意のオブジェクトxにマッピングします。
(分類子)クラスyを任意のオブジェクトxにマッピングします。
このメソッドは元々バイナリ分類子を参照しますが、複数分類タスクで機能させる方法があります。
次の簡単な例でメソッドの概念を説明すると便利です。平面上の点は2つのクラスに分割されます(図1)。 これら2つのクラスを分割する線を描画します(図1の赤い線)。 さらに、すべての新しいポイント(トレーニングセットからではない)は、次のように自動的に分類されます。
線の上の点はクラスAに分類され、
線の下の点はクラスBにあります。
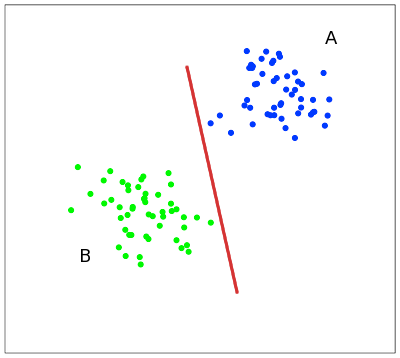
このような線を分割線と呼びます。 ただし、高次元のスペースでは、「線の下」または「線の上」の概念がすべての意味を失うため、直線がクラスを分離しなくなります。 したがって、線ではなく、超平面(元の空間の寸法よりも1つ小さい寸法の空間)を考慮する必要があります。 で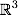 たとえば、超平面は通常の2次元平面です。
たとえば、超平面は通常の2次元平面です。
この例では、2つのクラスを分離するいくつかの行があります(図2)。

分類精度の観点から、各クラスまでの距離が最大である直線を選択することが最善です。 つまり、クラスを最良の方法で分割する線を選択します(図2の赤い線)。 このような直線、および一般的な場合は超平面は、最適な分離超平面と呼ばれます。
分割超平面に最も近いベクトルは、サポートベクトルと呼ばれます。 図2では、赤でマークされています。
トレーニングサンプルがあるとします。 。
。
サポートベクトルメソッドは、次の形式で分類関数Fを構築します。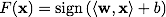 、
、
どこで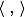 スカラー積、 wは分割超平面の法線ベクトル、 bは補助パラメーターです。 F( x )= 1のオブジェクトは1つのクラスに分類され、 F( x )= -1のオブジェクトは別のクラスに分類されます。 まさにそのような関数の選択は偶然ではありません:超平面は次の形式で指定できます
スカラー積、 wは分割超平面の法線ベクトル、 bは補助パラメーターです。 F( x )= 1のオブジェクトは1つのクラスに分類され、 F( x )= -1のオブジェクトは別のクラスに分類されます。 まさにそのような関数の選択は偶然ではありません:超平面は次の形式で指定できます 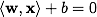 いくつかのwとb
いくつかのwとb
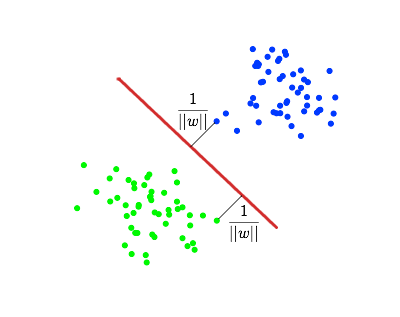
次に、各クラスまでの距離を最大にするwとbを選択します。 この距離は次と等しいと計算できます。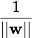 。 最大値を見つける問題
。 最大値を見つける問題  最小値を見つける問題と同等
最小値を見つける問題と同等  。 これらすべてを最適化問題の形式で記述します。
。 これらすべてを最適化問題の形式で記述します。

これは標準の二次計画問題であり、ラグランジュ乗数を使用して解決されます。 この方法の説明は、Wikipediaにあります。
実際には、データを超平面で区切ることができる場合、または言われているように線形である場合は非常にまれです。 線形の分離不可能性の例を図3に示します。

この場合、彼らはこれを行います:トレーニングセットのすべての要素は、特別なマッピングを使用して、より高い次元の空間Xに埋め込まれます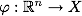 。 さらに、マッピング
。 さらに、マッピング 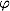 は、新しい空間Xでサンプルが線形に分離できるように選択されます。
は、新しい空間Xでサンプルが線形に分離できるように選択されます。
分類関数Fは次の形式を取ります。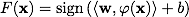 。 表現
。 表現 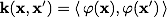 分類子のコアと呼ばれます。 数学的観点から見ると、カーネルは2つの変数の任意の正定対称関数です。 最適化問題の対応するラグランジュ関数が以下に制限されるように、正定性が必要です。 最適化タスクは正しく定義されます。
分類子のコアと呼ばれます。 数学的観点から見ると、カーネルは2つの変数の任意の正定対称関数です。 最適化問題の対応するラグランジュ関数が以下に制限されるように、正定性が必要です。 最適化タスクは正しく定義されます。
分類器の精度は、特にコアの選択に依存します。 ビデオでは、多項式コアを使用した分類の図を見ることができます。
ほとんどの場合、実際には次のカーネルが見つかります。
多項式: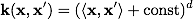
放射基底関数: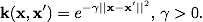
ガウス動径基底関数:
シグモイド: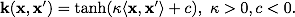
他の分類子の中でも、Relevance Vector Machine(RVM)メソッドにも注目したいと思います。 SVMとは異なり、このメソッドは、オブジェクトがこのクラスに属する確率を提供します。 つまり SVMが「 xはクラスAに属する」と言う場合、RVMは「 xは確率pでクラスAに属し、クラスBは確率1-pで属する」と言います。
1. クリストファーM.ビショップ。 パターン認識と機械学習、 2006。
2. K.V. Vorontsov。 サポートベクターの方法に関する講義。
この記事では、サポートベクターマシン(サポートベクターマシン、SVM)によるデータ分類の問題について説明します。 この分類には、パターン認識やスパムフィルターの作成から、ロケット排気ガス中の高温アルミニウム粒子の分布の計算まで、かなり幅広い用途があります。
最初に、元のタスクに関するいくつかの言葉。 分類タスクは、少なくとも2つの初期既知オブジェクトのどのクラスが属するかを判別することです。 通常、そのようなオブジェクトはn次元の実空間のベクトルです
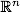 。 ベクトルの座標は、オブジェクトの個々の属性を表します。 たとえば、RGBモデルで指定された色cは、3次元空間のベクトルです: c =( red、green、blue )。
。 ベクトルの座標は、オブジェクトの個々の属性を表します。 たとえば、RGBモデルで指定された色cは、3次元空間のベクトルです: c =( red、green、blue )。
2つのクラス(「スパム/スパムではない」、「クレジットを与える/クレジットを与えない」、「赤/黒」)しかない場合、タスクはバイナリ分類と呼ばれます。 複数のクラスがある場合-マルチクラス(マルチクラス)分類。 また、各クラスのサンプルが存在する場合があります。どのクラスに属しているかが事前にわかっているオブジェクトです。 このようなタスクは教師による学習と呼ばれ、既知のデータはトレーニングサンプルと呼ばれます 。 (注:クラスが最初に定義されていない場合、クラスタリングのタスクがあります。 )
この記事で検討しているサポートベクターの方法は、教師による指導に関連しています。
したがって、分類問題の数学的定式化は次のとおりです。Xをオブジェクトの空間とします(たとえば、
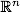 )、 Yはクラスです(たとえば、 Y = {-1,1})。 与えられたトレーニングサンプル:
)、 Yはクラスです(たとえば、 Y = {-1,1})。 与えられたトレーニングサンプル: 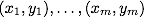 。 関数を構築する必要があります
。 関数を構築する必要があります 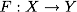 (分類子)クラスyを任意のオブジェクトxにマッピングします。
(分類子)クラスyを任意のオブジェクトxにマッピングします。
サポートベクター法
このメソッドは元々バイナリ分類子を参照しますが、複数分類タスクで機能させる方法があります。
メソッドのアイデア
次の簡単な例でメソッドの概念を説明すると便利です。平面上の点は2つのクラスに分割されます(図1)。 これら2つのクラスを分割する線を描画します(図1の赤い線)。 さらに、すべての新しいポイント(トレーニングセットからではない)は、次のように自動的に分類されます。
線の上の点はクラスAに分類され、
線の下の点はクラスBにあります。

このような線を分割線と呼びます。 ただし、高次元のスペースでは、「線の下」または「線の上」の概念がすべての意味を失うため、直線がクラスを分離しなくなります。 したがって、線ではなく、超平面(元の空間の寸法よりも1つ小さい寸法の空間)を考慮する必要があります。 で
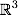 たとえば、超平面は通常の2次元平面です。
たとえば、超平面は通常の2次元平面です。
この例では、2つのクラスを分離するいくつかの行があります(図2)。

分類精度の観点から、各クラスまでの距離が最大である直線を選択することが最善です。 つまり、クラスを最良の方法で分割する線を選択します(図2の赤い線)。 このような直線、および一般的な場合は超平面は、最適な分離超平面と呼ばれます。
分割超平面に最も近いベクトルは、サポートベクトルと呼ばれます。 図2では、赤でマークされています。
ちょっとした数学
トレーニングサンプルがあるとします。
 。
。
サポートベクトルメソッドは、次の形式で分類関数Fを構築します。
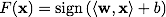 、
、
どこで
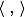 スカラー積、 wは分割超平面の法線ベクトル、 bは補助パラメーターです。 F( x )= 1のオブジェクトは1つのクラスに分類され、 F( x )= -1のオブジェクトは別のクラスに分類されます。 まさにそのような関数の選択は偶然ではありません:超平面は次の形式で指定できます
スカラー積、 wは分割超平面の法線ベクトル、 bは補助パラメーターです。 F( x )= 1のオブジェクトは1つのクラスに分類され、 F( x )= -1のオブジェクトは別のクラスに分類されます。 まさにそのような関数の選択は偶然ではありません:超平面は次の形式で指定できます 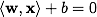 いくつかのwとb
いくつかのwとb

次に、各クラスまでの距離を最大にするwとbを選択します。 この距離は次と等しいと計算できます。
 。 最大値を見つける問題
。 最大値を見つける問題  最小値を見つける問題と同等
最小値を見つける問題と同等  。 これらすべてを最適化問題の形式で記述します。
。 これらすべてを最適化問題の形式で記述します。

これは標準の二次計画問題であり、ラグランジュ乗数を使用して解決されます。 この方法の説明は、Wikipediaにあります。
線形不可分性
実際には、データを超平面で区切ることができる場合、または言われているように線形である場合は非常にまれです。 線形の分離不可能性の例を図3に示します。

この場合、彼らはこれを行います:トレーニングセットのすべての要素は、特別なマッピングを使用して、より高い次元の空間Xに埋め込まれます
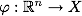 。 さらに、マッピング
。 さらに、マッピング 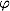 は、新しい空間Xでサンプルが線形に分離できるように選択されます。
は、新しい空間Xでサンプルが線形に分離できるように選択されます。
分類関数Fは次の形式を取ります。
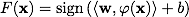 。 表現
。 表現 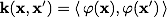 分類子のコアと呼ばれます。 数学的観点から見ると、カーネルは2つの変数の任意の正定対称関数です。 最適化問題の対応するラグランジュ関数が以下に制限されるように、正定性が必要です。 最適化タスクは正しく定義されます。
分類子のコアと呼ばれます。 数学的観点から見ると、カーネルは2つの変数の任意の正定対称関数です。 最適化問題の対応するラグランジュ関数が以下に制限されるように、正定性が必要です。 最適化タスクは正しく定義されます。
分類器の精度は、特にコアの選択に依存します。 ビデオでは、多項式コアを使用した分類の図を見ることができます。
ほとんどの場合、実際には次のカーネルが見つかります。
多項式:
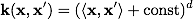
放射基底関数:
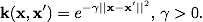
ガウス動径基底関数:

シグモイド:
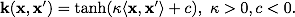
結論と文献
他の分類子の中でも、Relevance Vector Machine(RVM)メソッドにも注目したいと思います。 SVMとは異なり、このメソッドは、オブジェクトがこのクラスに属する確率を提供します。 つまり SVMが「 xはクラスAに属する」と言う場合、RVMは「 xは確率pでクラスAに属し、クラスBは確率1-pで属する」と言います。
1. クリストファーM.ビショップ。 パターン認識と機械学習、 2006。
2. K.V. Vorontsov。 サポートベクターの方法に関する講義。
All Articles