「日常」アプリケーションでの離散数学
昨日のシリーズでは、フューチュラムはかなり興味深いタスクを提起しました-ここでそれを分解せざるを得ませんでした。

そのため、プロットは次のようになります。教授は、身体を交換するための機械を発明しました。 いくつかの順列の後、英雄たちは自分の体に戻る方法を考え出さなければならないという困難な状況に陥りました。 これは「純粋な数学」が私たちを助ける場所です。
それでは始めましょう。 させる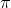 セット[n] = {1 ... n}の長さkのサイクルです。 一般性を失うことなく、次のように記述します。
セット[n] = {1 ... n}の長さkのサイクルです。 一般性を失うことなく、次のように記述します。

(a、b)をaとbの内容を入れ替える転置とする。
仮定により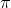 [n]上の特定の順列を使用して取得されます。
[n]上の特定の順列を使用して取得されます。
2つの「新しいボディ」 {x、y}を導入して、

i = 1、... kの場合、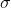 一連の順列として:
一連の順列として:
(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
転置は{x、y}の要素を持つ[n]の要素を変更するため、すべての転置は初期順列を形成したものとは異なることに注意してください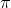 、および転置(x、y)から 。 簡単なチェックで得られること:
、および転置(x、y)から 。 簡単なチェックで得られること:

このように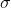 長さkのサイクルを反転し、転置(x、y)を使用せずにxとyを再配置したままにします。
長さkのサイクルを反転し、転置(x、y)を使用せずにxとyを再配置したままにします。
さあ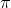 -ランダム置換; 独立したサイクルの構成に分割されます。各サイクルは、上記で取得したアルゴリズムを使用して反転できます。その後、必要に応じて、転置(x、y)を使用してxとyを交換できます。
-ランダム置換; 独立したサイクルの構成に分割されます。各サイクルは、上記で取得したアルゴリズムを使用して反転できます。その後、必要に応じて、転置(x、y)を使用してxとyを交換できます。
そうです。 また、ディスクリートにはIRLアプリケーションがありません。

そのため、プロットは次のようになります。教授は、身体を交換するための機械を発明しました。 いくつかの順列の後、英雄たちは自分の体に戻る方法を考え出さなければならないという困難な状況に陥りました。 これは「純粋な数学」が私たちを助ける場所です。
それでは始めましょう。 させる
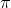 セット[n] = {1 ... n}の長さkのサイクルです。 一般性を失うことなく、次のように記述します。
セット[n] = {1 ... n}の長さkのサイクルです。 一般性を失うことなく、次のように記述します。

(a、b)をaとbの内容を入れ替える転置とする。
仮定により
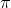 [n]上の特定の順列を使用して取得されます。
[n]上の特定の順列を使用して取得されます。
2つの「新しいボディ」 {x、y}を導入して、

i = 1、... kの場合、
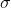 一連の順列として:
一連の順列として:
(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
転置は{x、y}の要素を持つ[n]の要素を変更するため、すべての転置は初期順列を形成したものとは異なることに注意してください
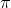 、および転置(x、y)から 。 簡単なチェックで得られること:
、および転置(x、y)から 。 簡単なチェックで得られること:

このように
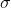 長さkのサイクルを反転し、転置(x、y)を使用せずにxとyを再配置したままにします。
長さkのサイクルを反転し、転置(x、y)を使用せずにxとyを再配置したままにします。
さあ
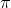 -ランダム置換; 独立したサイクルの構成に分割されます。各サイクルは、上記で取得したアルゴリズムを使用して反転できます。その後、必要に応じて、転置(x、y)を使用してxとyを交換できます。
-ランダム置換; 独立したサイクルの構成に分割されます。各サイクルは、上記で取得したアルゴリズムを使用して反転できます。その後、必要に応じて、転置(x、y)を使用してxとyを交換できます。
そうです。 また、ディスクリートにはIRLアプリケーションがありません。
All Articles