1000倍のパスワードハッシュの暗号強度

このトピックで生じた、パスワードに対するハッシュの繰り返し使用の暗号化強度に関する議論（ちなみに、他のフォーラムでのスリップ）により、私はこれに少し数学的なトピックを押し付けました。 問題の本質は、 遅い検証アルゴリズムを取得するためにパスワードを暗号アルゴリズム（ほとんどの場合ハッシュ関数）で保存する前に繰り返し（1,000回以上）処理するという考えから生じ、それにより攻撃者による傍受または盗難の場合のブルートフォースに効果的に対抗します。値。 Scratch （最初の記事の著者）の右利きのユーザーとして、 mrTheとIlyaPodkopaevは 、このアイデアは新しいものではなく、Cisco機器、RARアーカイバーなどの開発者によって使用されていると指摘しました。 しかし、ハッシュは多数の値を圧縮する操作であるため、完全に論理的な疑問が生じます。システムの安定性を損ないますか？ この質問に答えようとするのは



2つの脅威モデルの回復力の低下を検討します。

1. 攻撃者は、値空間の狭小化による衝突を見つけることを期待して、ランダムな入力バイトセットを列挙します（「完全列挙」）。
2. 辞書を検索します。

最初の、より理論的な質問から始めましょう。 「現代のハッシュ関数2 ¹²⁸ （MD5）、2 ¹⁶⁰ （SHA-1）、2 ²⁵⁶ （GOST R 34.11、SHA-256）の値のこのような巨大なスペースは、繰り返し使用することで絞り込めますか単純なランダム検索で衝突を検出できる程度まで？」

開始する

暗号化ハッシュ関数の主な特性/要件の1つは、出力結果の非常に優れた均一な分布です。 これにより、確率と組み合わせ論の通常の理論により、以下で必要とされる推定値で操作することができます。



N個の要素の入力セットと、 N個のオブジェクトの出力セットで比較する各オブジェクトをランダムな要素としてみましょう（図を参照）。 明らかに、いくつかのマッピングでは同じ要素が表示されるため、単一の矢印に収まらない要素が残ります。







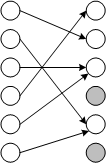
出力セットの特定の要素が特定のマッピング（矢印）によって選択されない確率は 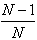、したがって、彼がN個の矢印のいずれによっても選択されない確率は、 または何が同じですか （暗号化ハッシュ関数の特性により、すべてのNマッピングは最初の近似では独立したイベントです）。



制限 2番目の顕著な制限の結果であり、 、つまり 約0.3679。 これは、出力セットの要素が「灰色になる」確率です。 途中で、 Nが大きい（2 ^32を超える）場合、「劣化」の程度はハッシュ関数の容量に依存しないことに注意してください。 その結果、最初のハッシュの繰り返し後、値スペースの約63％だけが残ります。 すべてがさらに進んだ場合、それは災害になります。たった150回の反復で、100ビットの出力スペースを「食べ」、例えばMD5に2 ^128-100 = 2 ²⁸オプションだけを残します。 幸いなことに、これはそうではありません。

詳細に

入力セットが不完全になるとすぐに（つまり、最初の脅威モデルでの2回目の反復の後、または2番目の脅威モデルで（辞書攻撃を使用して）すぐに）、他の式と他のパターンが機能し始めます。 これは、入力セットに「アクティブな」要素が3つしかなかった場合の同じ図に明確に見られます。 要素が「失われる」（出力セットが狭くなる）確率は急激に低下します。 現在では、同じ要素で2つ以上のマッピングが発生する頻度はかなり低くなっています。







入力セットでkN個の要素のみをアクティブにします（ 0 <k <1） 。 その場合、特定の要素を選択しない確率は 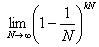、に等しい 、およびこの反復での出力セットの絞り込みは 。 以下は、最初の6回の反復の表です。

繰り返し数、i	値のセットの端数k
1	1,0000
2	0.6321
3	0.4685
4	0.3740
5	0.3120
6	0.2680

もちろん、アクティブな要素の割合は反復ごとに減少し続けますが、最初のときほど迅速かつ壊滅的ではありません。



多数の反復で抵抗の減少の程度を評価するには、数k自体ではなく、その逆-基数2の対数スケールで出力セットが何回減少したかを調べて、ビットが単位になるようにするのがより便利です： 。 徹底的な検索に対する耐性の低下を特徴付けるのはこの数値です。安定したハッシュ関数に相当するビット深度を得るには、選択したハッシュ関数のビット深度から減算する必要があります。 50,000回までの反復のrのプロットを図に示します。







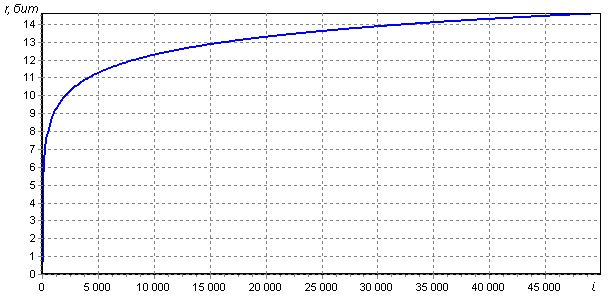
グラフが整数rの値と交差する点は、表にまとめられています。

耐久性の低下、r（ビット）	反復回数、i
4	30
5	61
6	125
7	253
8	509
9	1.020
10	2.044
11	4.092
12	8.188
13	16.379
14	32.763
15	65.531
16	131.067
...	...
20	2.097.146
...	...
24	33.554.425

ご覧のとおり、ある瞬間からの抵抗の減少は非常にゆっくりと増加します。 さらに、反復回数は2のべき乗に正確に従います。 。 同様のパターンが観察されるすべての場合において、それらは分析的に証明できますが、私はそれを目標として設定しませんでした。 したがって、アルゴリズムの安定性を16ビット以上に低下させることなく（128ビットハッシュ関数についての私の意見では、これは今後25年間の実際の安定性に影響を与えません）、パスワードハッシュの130,000回の反復を実行できます。 256ビットのハッシュ関数（SHA-256、GOST R 34.11、RIPEMD-256など）の場合、明らかにこのバーは何倍も高くなります。

モデルの妥当性チェック

いつものように、多数の理論的作成の後、得られた理論が実際からどれだけ離れているかを少なくとも何らかの形で評価したいという要望があります。 実験的なハッシュ関数として、MD5から最初の16ビットを取得しました（暗号化ハッシュ関数を使用すると、結果ビットのセットを選択して、同様のプロパティを持つ切り捨てられたハッシュ関数を形成できますが、もちろん、新しいビット深度に対応して抵抗は小さくなります）。 0から0xFFFFまでのすべての可能な値がアルゴリズムの入力に供給され、各値に対してi回の反復が実行されます。各反復は、MD5結果の最初の16ビットの計算にあります（16ビットのハッシュ関数が取得されます）。 「実験の結果」を表に示します。

計画抵抗低減、r（ビット）	反復回数、i	セット内の予想される要素の数	セット内の観測された要素の数
4	30	2 16-4 = 4.096	3.819
6	125	2 16-6 = 1.024	831
8	509	2 16-8 = 256	244

もちろん、 Nのような小さな値、特にkNでは、上記のすべての計算が制限に対して与えられているという事実がすぐに影響し始めます（ Nに匹敵し、大きい2 ^128-すべてがそこにあります）。 しかし、ここでも、一般的な傾向をたどることができ、上記で得られた式に受け入れられるようになります。

結果-辞書攻撃に対する抵抗

「辞書または簡単に作成できるパスワードがパスフレーズとして選択されている場合、値の範囲の狭まりは顕著ですか？」と分析する時が来ました。 明らかに、この場合、値の「アクティブな」入力セットはすでに極端に狭められています-2 ^{16〜2 48の}範囲の選択方法に依存します。 したがって、スケジュールの右側の「退院した」状況にすぐに気づきます。 ここでは、2つの異なる入力要素を同じ出力にマッピングする確率は非常に小さいです。 何百万および何百万もの操作によって、出力セットの要素の数はほとんど変わりません。 単位/数十が排除されます-音声の安定性の実用的な低下の問題はありません。

結論

説明されているブルートフォース保護スキームは、実際には暗号強度に実質的に制限なく自由に適用できます。 推奨される反復回数の上限（許容される抵抗rの減少は、ハッシュ関数の_1/8ビットの量^で主観的に選択されます）を表に示します。

ビット深度ハッシュ関数（ビット）	許容される抵抗の減少、r（ビット）	許可された反復回数の上限i
128	16	130,000
160	20	2,000,000
192	24	32.000.000
224	28	500,000,000
256	32	8.000.000.000