गतिशील प्रोग्रामिंग। शास्त्रीय कार्य

नमस्कार, हबहार। मैं वर्तमान में ओलंपियाड प्रोग्रामिंग पर एक पाठ्यपुस्तक पर काम कर रहा हूं, जिसमें से एक अनुभाग गतिशील प्रोग्रामिंग के लिए समर्पित है। इस पैराग्राफ का एक अंश निम्नलिखित है। इस विषय को यथाशीघ्र समझाने की कोशिश करते हुए, मैंने दृष्टांतों के साथ मुश्किल क्षणों का सामना करने की कोशिश की। मुझे आपकी राय में दिलचस्पी है कि यह सामग्री कैसे समझी जा सकती है। इस खंड में अन्य कार्यों को क्या शामिल किया जाना चाहिए, इस पर सलाह के साथ मुझे भी खुशी होगी।



कई ओलिंपियाड प्रोग्रामिंग समस्याओं में, पुनरावृत्ति या संपूर्ण खोज का उपयोग करके एक समाधान के लिए बहुत बड़ी संख्या में संचालन की आवश्यकता होती है। इस तरह की समस्याओं को हल करने का प्रयास, उदाहरण के लिए, संपूर्ण खोज द्वारा, अतिरिक्त निष्पादन समय की ओर जाता है।



हालांकि, संपूर्ण और कुछ अन्य समस्याओं के बीच, कोई भी व्यक्ति उन समस्याओं के एक वर्ग को अलग कर सकता है जिनके पास एक अच्छी संपत्ति है: कुछ उपप्रकारों के समाधान (उदाहरण के लिए, एक छोटी संख्या n के लिए ), यह संभव है कि बिना किसी रुकावट के लगभग मूल समस्या का हल खोजा जाए।



इस तरह की समस्याओं को डायनेमिक प्रोग्रामिंग की विधि द्वारा हल किया जाता है, और डायनेमिक प्रोग्रामिंग द्वारा ही किसी समस्या को घटाना घटाना है।

दृश्यों

एक अनुक्रम में शास्त्रीय समस्या निम्नलिखित है।



फाइबोनैचि अनुक्रम F _n सूत्रों द्वारा दिया गया है: F ₁ = 1, F ₂ = 1,

F _n = F _{n - 1} + F _{n - 2} for n > 1. संख्या n द्वारा F _n ज्ञात करना आवश्यक है।



एक समाधान जो तार्किक और कुशल लग सकता है वह है पुनरावृत्ति-आधारित समाधान:

 int F (इंट एन) {
  if (n <2) वापसी 1;
  और वापसी F (n - 1) + F (n - 2);
 } 

इस तरह के एक फ़ंक्शन का उपयोग करके, हम समस्या को "अंत से" हल करेंगे - जब तक हम ज्ञात मूल्यों तक नहीं पहुंचते हैं, तब तक हम कदम कम करते जाएंगे।



लेकिन जैसा कि आप देख सकते हैं, ऐसा प्रतीत होता है कि सरल प्रोग्राम पहले से ही n = 40 के साथ लंबे समय तक काम करता है। यह इस तथ्य के कारण है कि एक ही मध्यवर्ती डेटा की गणना कई बार की जाती है - संचालन की संख्या उसी दर से बढ़ती है जैसे फाइबोनैचि संख्या बढ़ती है - तेजी से।



इस स्थिति से बाहर निकलने का एक तरीका यह है कि मध्यवर्ती परिणाम पहले से ही उनके पुन: उपयोग के उद्देश्य से प्राप्त किए जाएं:

 int F (इंट एन) {
  अगर (ए [एन]! = -1) ए [एन] वापस;
  if (n <2) वापसी 1;
  और {
   ए [एन] = एफ (एन - 1) + एफ (एन - 2);
   वापसी ए [एन];
  }
 }

दिया गया समाधान सही और प्रभावी है। लेकिन इस कार्य के लिए, एक सरल उपाय लागू है:

 एफ [0] = 1;
 एफ [1] = 1;
 for (i = 2; i <n; i ++) F [i] = F [i - 1] + F [i - 2];

इस तरह के समाधान को "शुरुआत से" एक समाधान कहा जा सकता है - हम पहले ज्ञात मूल्यों को भरते हैं, फिर पहले अज्ञात मूल्य ( एफ ₃ ), फिर अगले, आदि का पता लगाते हैं, जब तक कि हम सही नहीं मिलते।



यह ऐसा समाधान है जो गतिशील प्रोग्रामिंग के लिए क्लासिक है: हमने पहले सभी उपप्रोमीटरों को हल किया (सभी _{i के} लिए i < n ) पाया, फिर, उपप्रोमीटर के समाधान को जानकर, हमने उत्तर पाया ( F _n = F _{n - 1} / F _{n - 2} , F _{n - 1} और एफ _{एन - 2} पहले से ही पाया गया है)।

एक आयामी गतिशील प्रोग्रामिंग

डायनेमिक प्रोग्रामिंग के सार को बेहतर ढंग से समझने के लिए, हम सबसे पहले किसी कार्य और एक उपवाक्य की अवधारणाओं को औपचारिक रूप से परिभाषित करेंगे।



प्रारंभिक समस्या n ₁ , n ₂ , ..., n _{k के} साथ कुछ संख्या T खोजने के लिए प्रारंभिक समस्या होने दें। यही है, हम फ़ंक्शन टी ( एन ₁ , एन ₂ , ..., एन _के ) के बारे में बात कर सकते हैं, जिसका मूल्य हमें उत्तर देने की आवश्यकता है। तब हम कार्यों को उपप्रकारों के रूप में मानेंगे

I ₁ < n ₁ , i ₂ < n ₂ , ..., i _k < _{k k के} लिए T ( i ₁ , i ₂ , ..., i _k )।



आगे हम क्रमशः k = 1, k = 2, k > 2 के लिए एक-आयामी, दो-आयामी और बहुआयामी गतिशील प्रोग्रामिंग के बारे में बात करेंगे।



एक आयामी गतिशील प्रोग्रामिंग का अगला कार्य विभिन्न रूपों में पाया जाता है।



समस्या 1. शून्य और लंबाई की इकाइयों के क्रम की संख्या की गणना करें जिसमें दो लगातार इकाइयाँ नहीं होती हैं।



N <32 के लिए, एक पूर्ण गणना के लिए कई सेकंड की आवश्यकता होगी, और n = 64 के लिए एक पूर्ण गणना सिद्धांत में संभव नहीं है। डायनेमिक प्रोग्रामिंग की विधि द्वारा समस्या को हल करने के लिए, हम मूल समस्या को घटाकर घटाते हैं।



N = 1, n = 2 के लिए, उत्तर स्पष्ट है। मान लीजिए कि हमने पहले से ही K _{n - 1} , K _{n - 2} को लंबाई n - 1 और n - 2 के ऐसे अनुक्रमों की संख्या दी है।



आइए देखें कि लंबाई n का एक क्रम क्या हो सकता है। यदि इसका अंतिम वर्ण 0 है, तो पहला n - 1 लंबाई का कोई नियमित क्रम है

n - 1 (शून्य या एक के साथ समाप्त होने पर कोई फर्क नहीं पड़ता - इसके बाद 0)। केवल K _{n - 1} ऐसे क्रम हैं। यदि अंतिम वर्ण 1 है, तो निश्चित वर्ण 0 के बराबर होना चाहिए (अन्यथा एक पंक्ति में दो इकाइयाँ होंगी), और पहली

n - 2 वर्ण - लंबाई n - 2 के किसी भी नियमित अनुक्रम, ऐसे अनुक्रमों की संख्या K _{n - 2 है} ।







इस प्रकार, K ₁ = 2, K ₂ = 3, K _n = K _{n - 1} + K _{n - 2} for n > 2. अर्थात, यह समस्या वास्तव में फाइबोनैचि संख्याओं को खोजने में कम कर देती है।

दो आयामी गतिशील प्रोग्रामिंग

क्लासिक दो-आयामी गतिशील प्रोग्रामिंग समस्या एक आयताकार क्षेत्र में मार्ग की समस्या है।

विभिन्न योगों में, मार्गों की संख्या की गणना करना या ऐसा मार्ग खोजना आवश्यक है जो एक अर्थ में सर्वश्रेष्ठ हो।



ऐसी समस्याओं के कुछ सूत्र यहां दिए गए हैं:



समस्या 2. आकार n * m कोशिकाओं के आयताकार क्षेत्र को देखते हुए। आप दाएं या नीचे लंबाई में एक सेल ले सकते हैं। गणना करें कि ऊपरी बाएं सेल से निचले दाएं तक आप कितने तरीके प्राप्त कर सकते हैं।



कार्य 3. आकार n * m कोशिकाओं के आयताकार क्षेत्र को देखते हुए। आप एक सेल को दाईं ओर, नीचे या तिरछे दाईं ओर ले जा सकते हैं। प्रत्येक कोशिका में एक निश्चित प्राकृतिक संख्या होती है। ऊपरी बाएं सेल से निचले दाएं तक जाना आवश्यक है। मार्ग का वजन सभी का दौरा किया कोशिकाओं से संख्या के योग के रूप में गणना की जाती है। न्यूनतम वजन वाला मार्ग खोजना आवश्यक है।



ऐसे सभी कार्यों के लिए, यह विशेषता है कि प्रत्येक अलग-अलग मार्ग एक ही सेल के साथ दो या अधिक बार नहीं गुजर सकते हैं।



आइए कार्य 2 पर अधिक विस्तार से विचार करें। आप निर्देशांक ( i , j ) के साथ कुछ सेल में ऊपर या बाईं ओर से आ सकते हैं, अर्थात, निर्देशांक वाले कोशिकाओं से ( i - 1, j ) और ( i , j - 1):







इस प्रकार, सेल के लिए ( i , j ) मार्गों की संख्या A [i] [j] के बराबर होगी

A [i - 1] [j] + A [i] [j - 1], अर्थात्, कार्य दो उप-प्रकारों के साथ होता है। इस कार्यान्वयन में, दो मापदंडों का उपयोग किया जाता है - i और j - इसलिए, जैसा कि इस समस्या पर लागू होता है, हम दो आयामी गतिशील प्रोग्रामिंग के बारे में बात कर रहे हैं।



अब हम सरणी A की पंक्तियों (या स्तंभों) के माध्यम से क्रमिक रूप से जा सकते हैं, उपरोक्त सूत्र का उपयोग करके वर्तमान सेल के लिए मार्गों की संख्या का पता लगा सकते हैं। पहले, संख्या 1 को A [0] [0] में रखा जाना चाहिए।



समस्या 3 में, हम निर्देशांक के साथ कोशिकाओं से निर्देशांक ( i , j ) के साथ सेल में प्राप्त कर सकते हैं

( i - 1, j), ( i , j - 1) और ( i - 1, j - 1)। मान लीजिए कि इन तीन कोशिकाओं में से प्रत्येक के लिए हमने पहले से ही न्यूनतम वजन का मार्ग ढूंढ लिया है, और हमने डब्ल्यू [i - 1] [जे], डब्ल्यू [आई] [जे - १] में वजन रखा है,

डब्ल्यू [i - 1] [जे - १]। ( I , j ) के लिए न्यूनतम वजन खोजने के लिए, आपको न्यूनतम वजन W [i - 1] [j], W [i] [j - 1], W [i - 1] [j - 1] का चयन करना होगा और इसमें जोड़ना होगा। उसे वर्तमान सेल में दर्ज संख्या:



W [i] [j] = min (W [i - १] [j], W [i] [j - १], W [i - १] [j - १]) + A [i] [j] ;



यह कार्य इस तथ्य से जटिल है कि न केवल न्यूनतम वजन, बल्कि स्वयं मार्ग भी खोजना आवश्यक है। इसलिए, एक अन्य सरणी में, हम प्रत्येक सेल के लिए अतिरिक्त रूप से लिखेंगे, जिस पक्ष में हमें जाने की आवश्यकता है।



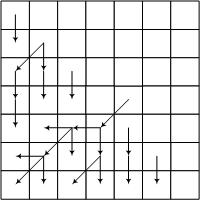
निम्न आंकड़ा स्रोत डेटा और एल्गोरिथ्म के चरणों में से एक का एक उदाहरण दिखाता है।







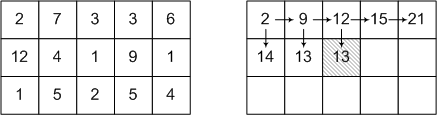
वास्तव में एक तीर पहले से ही पारित कोशिकाओं में से प्रत्येक में जाता है। यह तीर दिखाता है कि सेल में दर्ज न्यूनतम वजन प्राप्त करने के लिए आपको किस सेल में आने की आवश्यकता है।



पूरे सरणी से गुजरने के बाद, विपरीत दिशा में तीर का पालन करते हुए, आखिरी सेल से ही मार्ग का पता लगाना आवश्यक होगा।

बाद के कार्य

बाद में बढ़ने की समस्या पर विचार करें।



समस्या 4. पूर्णांकों का एक क्रम दिया गया है। इसके सबसे लंबे समय तक सख्ती से बढ़ते क्रम को खोजना आवश्यक है।



आइए शुरू से ही समस्या को हल करना शुरू करें - हम इस क्रम के पहले सदस्यों के साथ शुरू करते हुए, उत्तर की तलाश करेंगे। प्रत्येक संख्या i के लिए, हम स्थिति i पर एक तत्व में समाप्त होने वाले सबसे बड़े बढ़ते परिणाम की खोज करेंगे। प्रारंभिक अनुक्रम को सरणी ए में संग्रहीत किया जाता है। सरणी एल में हम वर्तमान तत्व के साथ समाप्त होने वाले अधिकतम बाद की लंबाई रिकॉर्ड करेंगे। मान लें कि हम सभी L [i] को 1 <= i <= k - 1. के लिए पाते हैं। अब हम L [k] को निम्न प्रकार से पा सकते हैं। हम 1 <= i < k - 1. के लिए सभी तत्वों ए [i] के माध्यम से देखते हैं

A [i] <A [k], तो kth तत्व A [i] में बाद के अंत का एक निरंतरता हो सकता है। प्राप्त किए गए परिणाम की लंबाई एल [i] से 1 अधिक होगी। L [k] को खोजने के लिए, सभी को 1 से k - 1 तक हल करना आवश्यक है:

L [k] = max (L [i]) + 1, जहां अधिकतम को सभी i पर लिया जाता है जैसे कि A [i] <A [k] और

1 <= i < k ।



यहां, खाली सेट का अधिकतम 0. के बराबर माना जाएगा। इस मामले में, मौजूदा तत्व चयनित अनुक्रम में केवल एक ही बन जाएगा, और पिछले वाले में से एक का एक निरंतरता नहीं होगा। सरणी एल में भरने के बाद, सबसे बड़ी बढ़ती बाद की लंबाई अधिकतम तत्व एल के बराबर होगी।



बाद में स्वयं को पुनर्स्थापित करने के लिए, प्रत्येक तत्व के लिए पिछले चयनित तत्व की संख्या को सहेजना संभव है, उदाहरण के लिए, एक सरणी में।



अनुक्रम 2, 8, 5, 9, 12, 6 के उदाहरण का उपयोग करके इस समस्या के समाधान पर विचार करें। चूंकि 2 तक कोई तत्व नहीं हैं, इसलिए अधिकतम अनुवर्ती में केवल एक तत्व होता है - एल [1] = 1, और इसके सामने एक भी नहीं है - एन [१] = ० आगे,

2 <8, इसलिए 8 पिछले तत्व के साथ अनुक्रम का एक निरंतरता हो सकता है। फिर एल [2] = 2, एन [2] = 1।







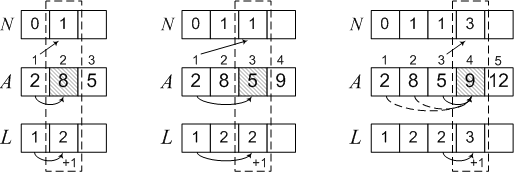
A [3] = 5 से कम केवल एक तत्व A [1] = 2 है, इसलिए 5 केवल एक परवर्ती की निरंतरता हो सकती है - एक जिसमें 2. समाहित है

L [3] = L [1] + 1 = 2, N [3] = 1, चूंकि 2 नंबर 1 के साथ स्थिति में है। इसी तरह, हम एल्गोरिथ्म के तीन और चरण करते हैं और अंतिम परिणाम प्राप्त करते हैं।







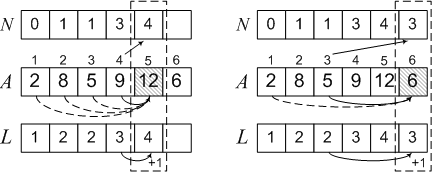
अब हम सरणी एल में अधिकतम तत्व का चयन करते हैं और सरणी एन से हम बाद में 2, 5, 9, 12 को पुनर्स्थापित करते हैं।



एक अन्य क्लासिक डायनामिक प्रोग्रामिंग समस्या पैलिंड्रोम समस्या है।



टास्क 5. लैटिन वर्णमाला के बड़े अक्षरों के एक स्ट्रिंग को देखते हुए। सबसे बड़े पलिंड्रोम की लंबाई का पता लगाना आवश्यक है, जिसे इस लाइन से कुछ अक्षरों को हटाकर प्राप्त किया जा सकता है।



हम इस लाइन को S, और इसके अक्षर S [i], 1 <= i <= n द्वारा दर्शाते हैं। हम इस स्ट्रिंग के संभावित पदार्थों पर विचार करेंगे- i से वें से j- वें वर्ण, हम उन्हें S ( i , j ) से दर्शाते हैं। सबस्ट्रिंग के लिए अधिकतम पालिंड्रोम्स की लंबाई एक वर्गाकार सरणी L: L [i] [j] में लिखी जाएगी, जो अधिकतम palindrome की लंबाई है, जिसे सब्स्ट्रिंग S ( i , j ) से प्राप्त किया जा सकता है।



आइए सरलतम पदार्थों के साथ समस्या को हल करना शुरू करें। एक वर्ण की स्ट्रिंग के लिए (अर्थात, S ( i , i ) फॉर्म का सबस्ट्रिंग), उत्तर स्पष्ट है - कुछ भी डिलीट करने की आवश्यकता नहीं है, ऐसा स्ट्रिंग एक पैलिंड्रोम होगा। दो वर्ण S ( i , i + 1) की एक स्ट्रिंग के लिए, दो विकल्प संभव हैं: यदि वर्ण समान हैं, तो हमारे पास एक palindrome है, कुछ भी हटाने की आवश्यकता नहीं है। यदि पात्र समान नहीं हैं, तो किसी को भी पार करें।



आइए अब हमें S ( i , j ) का विकल्प दिया गया है। यदि पहले (S [i]) और अंतिम (S [j]) सबस्ट्रिंग अक्षर मेल नहीं खाते हैं, तो उनमें से एक को निश्चित रूप से पार करना होगा। तब हमारे पास सबस्ट्रिंग S ( i , j - 1) या S ( i + 1, j ) होगा- यानी, हम समस्या को घटाकर घटा देंगे: L [i] [j] = अधिकतम (L [i] [j - 1] , L [i + 1] [j])। यदि पहले और अंतिम वर्ण समान हैं, तो हम दोनों को छोड़ सकते हैं, लेकिन हमें समस्या S ( i + 1, j - 1) का हल जानना होगा:

L [i] [j] = L [i + 1] [j - १] + २



उदाहरण के रूप में ABACCBA स्ट्रिंग का उपयोग करके समाधान पर विचार करें। सबसे पहले, इकाइयों के साथ सरणी के विकर्ण को भरें, वे एक वर्ण के एस ( i , i ) के अनुरूप होंगे। फिर हम लंबाई दो के सबस्ट्रिंग पर विचार करना शुरू करते हैं। सभी सबस्ट्रिंग में, S (4, 5) को छोड़कर, वर्ण अलग-अलग होते हैं, इसलिए हम संबंधित कोशिकाओं में 1 लिखते हैं, और 2 में L [4] [5]।



यह पता चला है कि हम सरणी को तिरछे से भरेंगे, मुख्य विकर्ण से शुरू होकर ऊपरी बाएं से निचले दाहिने तरफ। लंबाई 3 के सबस्ट्रिंग के लिए, निम्न मान प्राप्त किए जाते हैं: ए.बी.ए. को प्रतिस्थापित करने में, पहले और अंतिम अक्षर बराबर होते हैं

L [1] [3] = L [2] [2] + 2. शेष सबस्ट्रिंग में, पहले और अंतिम अक्षर अलग-अलग हैं।



बीएसी: एल [२] [४] = अधिकतम (एल [२] [३], एल [३] [४]) = १।

एसीसी: एल [३] [५] = अधिकतम (एल [३] [४], एल [४] [५]) = २।

CCB: L [4] [6] = मैक्स (L [4] [5], L [5] [6]) = 2।

CBA: L [5] [7] = मैक्स (L [5] [6], L [6] [7]) = 1।



इसी तरह के तर्क को आगे बढ़ाते हुए, हम सभी कोशिकाओं को विकर्ण के नीचे और सेल L [1] [7] = 6 में भरते हैं।







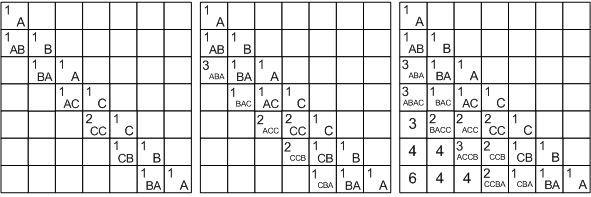
यदि समस्या में यह आवश्यक है कि लंबाई को न लें, लेकिन स्वयं पालिंड्रोम, तो लंबाई सरणी के अलावा हमें बदलाव की एक सरणी का निर्माण करना होगा - प्रत्येक कोशिका के लिए, याद रखें कि कौन से मामलों को कार्यान्वित किया गया था (आंकड़ा में, स्पष्टता के लिए, संख्यात्मक मानों को संक्रमणों के एन्कोडिंग के बजाय संबंधित तीर खींचे जाते हैं) ।