🤘 👂🏿 👼 नकली एनालिंग विधि 👩🏼‍🎤 🎉 🙍

प्रिय मित्रों, आपका दिन शुभ हो!

पहले से ही अधिक बार एक से अधिक अनुकूलन एल्गोरिदम जैसे आनुवंशिक एल्गोरिदम की यहां चर्चा की गई है। हालांकि, स्वतंत्रता के कई डिग्री के साथ समस्याओं में इष्टतम समाधान खोजने के अन्य तरीके हैं। उनमें से एक (और, यह कहा जाना चाहिए, सबसे प्रभावी में से एक) एनाउलिंग का एक तरीका है, जो अभी तक यहां चर्चा नहीं की गई है। मैंने इस अन्याय को खत्म करने और सबसे सरल संभव शब्दों में इस अद्भुत एल्गोरिदम से परिचित कराने का फैसला किया, और साथ ही एक साधारण समस्या को हल करने के लिए इसके उपयोग का एक उदाहरण दिया।

मैं समझता हूं कि आनुवंशिक एल्गोरिदम इतने लोकप्रिय क्यों हैं: वे बहुत कल्पनाशील हैं और इसलिए समझना आसान है। वास्तव में, कुछ गुणों के साथ जीवित प्राणियों की आबादी के विकास की एक वास्तविक जैविक प्रक्रिया के रूप में, किसी समस्या के समाधान को प्रस्तुत करना मुश्किल और बेहद दिलचस्प नहीं है। इस बीच, annealing एल्गोरिथम का वास्तविक दुनिया में भी अपना स्वयं का प्रोटोटाइप है (यह नाम से ही स्पष्ट है)। सच है, वह जीवविज्ञान से नहीं, बल्कि भौतिकी से आया था। इस एल्गोरिथ्म द्वारा नकल की जाने वाली प्रक्रिया ठंडा और जमने के दौरान एक पदार्थ द्वारा एक न्यूनतम ऊर्जा के साथ क्रिस्टलीय संरचना के गठन के समान होती है, जब कण उच्च तापमान पर बेतरतीब ढंग से चलते हैं, धीरे-धीरे सबसे कम ऊर्जा वाले स्थानों में धीमा और ठंड हो जाते हैं। केवल गणितीय समस्या के मामले में, पदार्थ के कणों की भूमिका मापदंडों द्वारा की जाती है, और ऊर्जा की भूमिका एक ऐसा कार्य है जो इन मापदंडों के सेट की इष्टतमता की विशेषता है।

शुरू करने के लिए, जो लोग भूल गए हैं, मैं आपको याद दिलाता हूं कि ऐसे विदेशी तरीकों से हम किस तरह के कार्यों को हल करने की कोशिश कर रहे हैं। ऐसे कई कार्य हैं जिनका सटीक समाधान बड़ी संख्या में परिवर्तनीय मापदंडों के कारण खोजना बहुत मुश्किल है। सामान्य मामले में, हमारे पास एक फ़ंक्शन एफ है, जिसकी न्यूनतम (अधिकतम) हमें खोजने की आवश्यकता है, और इसके मापदंडों का एक सेट X1..xn, जिनमें से प्रत्येक स्वतंत्र रूप से अपनी सीमा के भीतर भिन्न हो सकता है। पैरामीटर और, तदनुसार, फ़ंक्शन अलग-अलग और लगातार दोनों भिन्न हो सकते हैं। यह स्पष्ट है कि इस तरह के फ़ंक्शन के इनपुट डेटा पर एक जटिल निर्भरता होने की संभावना है, जिसमें कई स्थानीय मिनीमा हैं, जबकि हम एक वैश्विक न्यूनतम की तलाश कर रहे हैं। बेशक, हमेशा थकावट भरी खोज से समस्या को हल करने का विकल्प रहता है, लेकिन यह केवल असतत मामले में और बेहद सीमित इनपुट के साथ काम करता है। यह वह जगह है जहाँ अनुकूलन एल्गोरिदम खेलने में आते हैं।

शुष्क नहीं होने के लिए, मैं आपको तुरंत उस समस्या के बारे में बताऊंगा जो मैं इस लेख के ढांचे में हल करूंगा। कल्पना कीजिए कि एक चेकर बोर्ड की माप एल द्वारा की जाती है। कोशिका का किनारा एक के बराबर है। बोर्ड पर आपको एन बिंदुओं की ऐसी व्यवस्था खोजने की आवश्यकता है ताकि इन बिंदुओं को जोड़ने वाली न्यूनतम पॉलीलाइन की लंबाई अधिकतम हो। सामान्य न्यूनतम समस्या। जाहिर है, इस मामले में, फ़ंक्शन F अंक की एक निश्चित व्यवस्था के लिए न्यूनतम पॉलीलाइन की लंबाई मानता है, और इसके पैरामीटर बिंदुओं के x और y निर्देशांक हैं, अर्थात्। 2 * एन पैरामीटर।

दरअसल, एल्गोरिथ्म

तो, एक फ़ंक्शन है जो सिस्टम को चिह्नित करता है, और निर्देशांक का सेट जिस पर यह फ़ंक्शन दिया जाता है। सबसे पहले, आपको सिस्टम की प्रारंभिक स्थिति निर्धारित करने की आवश्यकता है। इसके लिए, बस किसी भी यादृच्छिक राज्य को लिया जाता है। अगला, हर kth कदम पर, हम

सबसे अच्छा पाया के साथ एफ के वर्तमान मूल्य की तुलना करें; यदि वर्तमान मूल्य बेहतर है - वैश्विक सबसे अच्छा बदलें
बेतरतीब ढंग से एक नया राज्य उत्पन्न; इसके लिए संभाव्यता वितरण वर्तमान स्थिति और वर्तमान तापमान पर निर्भर होना चाहिए
उत्पन्न बिंदु के लिए फ़ंक्शन के मूल्य की गणना करें
उत्पन्न स्थिति को वर्तमान के रूप में स्वीकार या नहीं करना; इस निर्णय की संभावना उत्पन्न और वर्तमान राज्यों के कार्यों के बीच अंतर पर निर्भर होनी चाहिए और निश्चित रूप से, तापमान पर (उच्च तापमान, वर्तमान स्थिति की तुलना में खराब स्थिति को स्वीकार करने की अधिक संभावना है)
यदि नया राज्य स्वीकार नहीं किया जाता है, तो हम एक और उत्पन्न करते हैं और तीसरे बिंदु से चरणों को दोहराते हैं, अगर स्वीकार किया जाता है, तो हम अगले पुनरावृत्ति पर आगे बढ़ते हैं, तापमान को कम करते हैं (लेकिन अधिक बार अगले चरण में संक्रमण किसी भी मामले में किया जाता है, लंबे लूप से बचने के लिए)

एक निश्चित तापमान तक पहुंचने पर प्रक्रिया रुक जाती है। पदार्थ न्यूनतम ऊर्जा के साथ एक बिंदु पर ठंडा हो गया है।

हमें बिंदु से बिंदु तक संक्रमण की संभावनाओं के साथ ऐसी जटिल योजना की आवश्यकता क्यों है? आप अधिक ऊर्जा से कम करने के लिए कड़ाई से कदम क्यों नहीं उठा सकते? यह सब पहले से ही वर्णित स्थानीय मिनीमा के बारे में है, जिसमें समाधान बस अटक सकता है। उनसे बाहर निकलने और एक न्यूनतम वैश्विक खोजने के लिए, सिस्टम की ऊर्जा बढ़ाने के लिए समय-समय पर आवश्यक है। इसी समय, कम से कम ऊर्जा की खोज करने की सामान्य प्रवृत्ति बनी हुई है। यह एनाउलिंग की पद्धति का सार है।

और फिर से बोर्ड पर डॉट्स के बारे में

अब जब एल्गोरिथ्म की सामान्य योजना स्पष्ट है, तो आइए अपने मेढ़े पर लौटें। हम टास्क को जावा में लागू करेंगे। सबसे पहले, हम उस पर डॉट्स के साथ एक बोर्ड का वर्णन करते हैं।

बोर्ड:

public class Board { private Point[] points; private int N; private int width; private int height; public Board(int n, int w, int h) { points = new Point[n]; N = n; width = w; height = h; } public Board(Board board) { points = new Point[board.points.length]; for (int i = 0; i < points.length; i++) points[i] = new Point(board.points[i].getX(), board.points[i].getY()); this.width = board.width; this.height = board.height; } public int getPointsCount() { return points.length; } public int getWidth() { return width; } public int getHeight() { return height; } public Point getPoint(int index) { return points[index]; } public void setPoint(int index, Point p) { points[index] = p; } }

और बिंदु:

 public class Point { private int x; private int y; public Point(int x, int y) { this.x = x; this.y = y; } public double dist(Point p) { return Math.sqrt((x - px) * (x - px) + (y - py) * (y - py)); } public void move(int dx, int dy, int xBorder, int yBorder){ if(((x + dx) < xBorder) && ((x + dx) >= 0)) x += dx; if(((y + dy) < yBorder) && ((y + dy) >= 0)) y += dy; } public int getX(){ return x; } public int getY(){ return y; } }

चूँकि अंकों का क्रम हमारे लिए वांछित कार्य की गणना के लिए महत्वपूर्ण है, हम उनके निर्धारित सेट का परिचय देते हैं:

 public class Polyline { public Point p[]; public int N = 5; public Polyline(int Num) { N = Num; p = new Point[N]; } public double dist() { double d = 0; for (int i = 0; i < (N - 1); i++) { d += p[i].dist(p[i + 1]); } return d; } }

अब हमें एक फ़ंक्शन F की आवश्यकता है, किसी दिए गए व्यवस्था की न्यूनतम पॉलीलाइन की तलाश और उसकी लंबाई की गिनती।

 public class MinPolyline { private double bestDist; private Polyline bestMinPolyl; private Board board; public Polyline F(Board b) { N = b.getPointsCount(); board = b; int[] perm = new int[N]; boolean used[] = new boolean[N]; for (int i = 0; i < N; i++) { perm[i] = i + 1; used[i] = false; } bestDist = Double.MAX_VALUE; permute (0, perm, used); return bestMinPolyl; } void permute(int first_index, int[] perm, boolean[] used) { if (first_index == N) { Polyline polyl = new Polyline(N); for (int i = 0; i < N; i++){ polyl.p[i] = board.getPoint(perm[i] - 1); } if (bestDist > polyl.dist()){ bestDist = polyl.dist(); bestMinPolyl = polyl; } return; } for (int i = 1; i < N+1; i++) { if (used[i - 1]) continue; perm[first_index] = i; used[i - 1] = true; permute(first_index + 1, perm, used); used[i - 1] = false; } } }

खैर, सारी तैयारी हो चुकी है। अब हम एल्गोरिथम को लागू करना शुरू कर सकते हैं।

एल्गोरिदम कार्यान्वयन

सामान्य योजना पर लौटते हुए, हम वहां निर्देशांक और तापमान के आधार पर दो वितरणों का उल्लेख करेंगे। उन्हें किसी तरह से परिभाषित करने की आवश्यकता है। इसके अलावा, हमें एक कानून की आवश्यकता है जिसके अनुसार तापमान परिवर्तन से पुनरावृत्ति में बदल जाएगा। इन तीन कार्यों को चुनने के बाद, हम एनालिंग विधि का एक ठोस आरेख बनाएंगे। मुझे कहना होगा कि एल्गोरिथ्म के कई संशोधन हैं जो वितरण और तापमान परिवर्तन के कानून द्वारा एक दूसरे से भिन्न होते हैं। उनके पास अपने पेशेवरों और विपक्ष हैं, जैसे गति, एक वैश्विक न्यूनतम खोजने की गारंटी, निष्पादन की जटिलता।

मैंने अपने कार्य के लिए चुना है एक संशोधन जिसे सुपरफास्ट एनीलिंग कहा जाता है। सबसे पहले, हम एक नए राज्य को अपनाने की संभावना वितरण का निर्धारण करते हैं।

या कोड में:

 h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T));

इस प्रकार, फ़ंक्शन के सबसे खराब परिणाम (उच्च ऊर्जा के साथ) के साथ स्थिति लेने की संभावना कम होती है, कम तापमान और वर्तमान ऊर्जा और इष्टतम एक के बीच का अंतर अधिक होता है। अगला, हम तापमान कम करने का कानून स्थापित करते हैं। अल्ट्राफास्ट एनीलिंग की एक विशिष्ट विशेषता यह है कि सभी निर्देशांक में परिवर्तन स्वतंत्र रूप से माना जाता है, और यहां तक कि प्रत्येक समन्वय के लिए तापमान अपने आप से निर्धारित होता है:

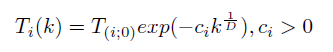
जहां D निर्देशांक की संख्या (यानी 2 * n) है, k चाल की संख्या है। हालांकि, सादगी के लिए, हम अभी भी सामान्य तापमान बनाते हैं:

 T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N)));

जैसा कि आप देख सकते हैं, तापमान तेजी से घट जाएगा, और प्रक्रिया जल्दी से समाप्त हो जाएगी।

अंत में, नए समन्वय के लिए वितरण। निम्नलिखित मूल्य एक समन्वय में सापेक्ष परिवर्तन को दर्शाता है:

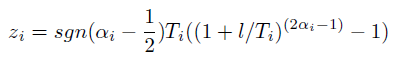
जहाँ अल्फा एक मात्रा है जो समान रूप से अंतराल पर वितरित की जाती है [0, 1]। यदि नया समन्वय इसके परिवर्तन के ढांचे में फिट नहीं होता है (हमारे मामले में, यह बोर्ड से परे है), तो गणना फिर से की जाती है।

 z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T; x = board.getPoint(moveNum).getX() + (int)(z * border);

अब हमारे पास सभी आवश्यक वितरण और कार्य हैं। यह केवल सब कुछ एक साथ रखने के लिए बनी हुई है। बोर्ड आयामों, अंकों की संख्या, प्रारंभिक और अंतिम तापमान और इनपुट डेटा के रूप में तापमान घातांक के क्षीणन क्षरण को स्थानांतरित करना आवश्यक है।

 public class AnnealingOptimizer { public int N; public int width; public int height; public AnnealingOptimizer(int n, int width, int height) { N = n; this.width = width; this.height = height; } public Board optimize(double To, double Tend, double decrement){ Board board = new Board(N, width, height); Board bestBoard = new Board(N, width, height); Random r = new Random(); double maxDist = 0; double T = To; double h; MinPolyline minPolyl = new MinPolyline(); for (int j = 0; j < N; ++j){ board.setPoint(j, new Point(r.nextInt(height), r.nextInt(width))); bestBoard.setPoint(j, board.getPoint(j)); } int i = 1; while (T > Tend){ for (int moveNum = 0; moveNum < board.getPointsCount(); ++moveNum){ NewX(board, moveNum, T, width, true); NewX(board, moveNum, T, height, false); } if (minPolyl.F(board).dist() > maxDist){ bestBoard = new Board(board); }else{ h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T)); if (r.nextDouble() > h){ board = new Board(bestBoard); }else{ bestBoard = new Board(board); } } maxDist = minPolyl.F(board).dist(); T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N))); ++i; } return bestBoard; } private void NewX (Board board, int moveNum, double T, int border, boolean xCoord) { Random r = new Random(); int x; double z; double alpha = r.nextDouble(); z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T; if (xCoord){ x = board.getPoint(moveNum).getX() + (int)(z * border); if ((x < border) && (x >= 0)) { board.getPoint(moveNum).move((int)(z * border), 0, width, height); } else { NewX(board, moveNum, T, border, xCoord); } } else { x = board.getPoint(moveNum).getY() + (int)(z * border); if ((x < border) && (x >= 0)) { board.getPoint(moveNum).move(0, (int)(z * border), width, height); } else { NewX(board, moveNum, T, border, xCoord); } } } }

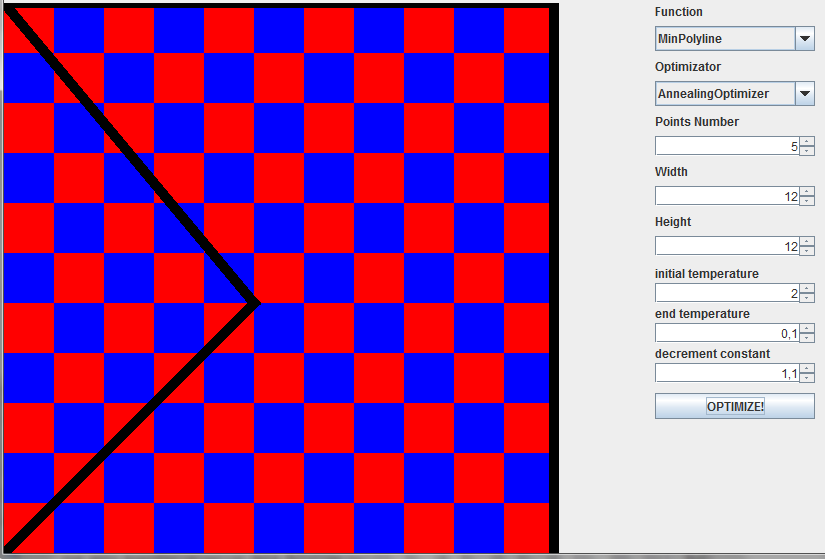
यह ध्यान दिया जाना चाहिए कि नकली एनालिंग विधि के कुछ संशोधन इष्टतम समाधान खोजने की सांख्यिकीय गारंटी प्रदान करते हैं। इसका मतलब है कि मापदंडों के सही विकल्प के साथ, एल्गोरिथ्म सभी इनपुटों के माध्यम से जाने के बिना उचित समय में इष्टतम समाधान ढूंढेगा। यह कार्यान्वयन 12x12 बोर्डों और लगभग 15,000 पुनरावृत्तियों में 5 बिंदुओं के लिए उत्तर पाता है। आपको याद दिला दूं कि प्लेसमेंट विकल्पों की कुल संख्या 12 ^ 10 है। जाहिर है, मापदंडों को समायोजित करने की कठिनाई लाभ के लायक है। वैसे, गति और सटीकता के संदर्भ में एनेलिंग की विधि कम से कम आनुवंशिक एल्गोरिथ्म से नहीं हारती है, लेकिन अधिक बार नहीं।

अंत में, एल्गोरिथ्म का दृश्य परिणाम।

प्रयुक्त साहित्य:

ए। लोपैटिन "एनीलिंग विधि"

नकली एनालिंग विधि

दरअसल, एल्गोरिथ्म

और फिर से बोर्ड पर डॉट्स के बारे में

एल्गोरिदम कार्यान्वयन

More articles: