प्रत्यक्ष फजी इंजेक्शन

परिचय

1965 में, पत्रिका "सूचना और नियंत्रण" ने एल। ज़ेडह के काम को "फ़ज़ी सेट्स" शीर्षक से प्रकाशित किया। इस नाम का रूसी में फ़ज़ी सेट के रूप में अनुवाद किया गया है । मकसद ऐसी घटनाओं और अवधारणाओं का वर्णन करने की आवश्यकता थी जो अस्पष्ट और गलत हैं। पहले से ज्ञात गणितीय विधियां जो शास्त्रीय सेट सिद्धांत और दो-मूल्यवान तर्क का उपयोग करती थीं, इस प्रकार की समस्याओं को हल करने की अनुमति नहीं देती थीं।







फ़ज़ी सेटों का उपयोग करके, कोई भी औपचारिक रूप से गलत और अस्पष्ट अवधारणाओं को परिभाषित कर सकता है, जैसे कि "उच्च तापमान" या "बड़ा तापमान"। फ़ज़ी सेट की परिभाषा तैयार करने के लिए, तर्क के तथाकथित क्षेत्र को निर्दिष्ट करना आवश्यक है। उदाहरण के लिए, जब हम किसी कार की गति का मूल्यांकन करते हैं, तो हम अपने आप को एक्स = [0, वीमैक्स] की सीमा तक सीमित कर देते हैं, जहां Vmax एक कार की अधिकतम गति विकसित हो सकती है। यह याद रखना चाहिए कि X एक स्पष्ट सेट है।

मूल अवधारणाएँ

कुछ गैर-रिक्त स्थान X में एक फ़ज़ी सेट A, जोड़े का सेट है



जहाँ



- एक फजी सेट ए की सदस्यता समारोह। यह फ़ंक्शन प्रत्येक तत्व एक्स को फजी सेट ए में इसकी सदस्यता की डिग्री प्रदान करता है।



पिछले उदाहरण को जारी रखते हुए, हम तीन गलत योगों पर विचार करते हैं:

- "कार की कम गति";

- "औसत वाहन गति";

- "हाई स्पीड कार।"

यह आंकड़ा सदस्यता कार्यों का उपयोग करते हुए उपरोक्त योगों के अनुसार फजी सेट दिखाता है।



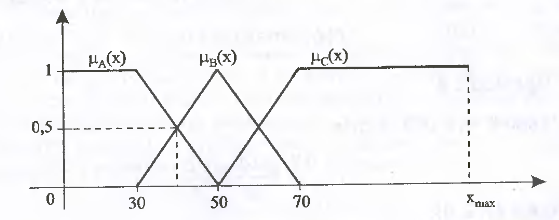
एक निश्चित बिंदु पर, X = 40 किमी / घंटा। फ़ज़ी सेट "लो स्पीड कार" का सदस्यता फ़ंक्शन 0.5 का मान लेता है। फ़ज़ी सेट की सदस्यता फ़ंक्शन "औसत वाहन की गति" एक ही मान मानती है, जबकि सेट के लिए "उच्च वाहन गति" इस बिंदु पर फ़ंक्शन का मान 0 है।



दो चर T: [0, 1] x [0, 1] -> [0, 1] के एक फ़ंक्शन T को T- मानदंड कहा जाता है यदि:

- दोनों तर्कों के संबंध में नहीं बढ़ रहा है: टी (ए, सी) <टी (बी, डी) के लिए <b, सी <डी;

- कम्यूटेटिव है: टी (ए, बी) = टी (बी, ए);

- जुड़ी हुई स्थिति को संतुष्ट करता है: टी (टी (ए, बी), सी) = टी (ए, टी (बी, सी));

- सीमा की स्थितियों को संतुष्ट करता है: टी (ए, 0) = 0, टी (ए, 1) = ए।

प्रत्यक्ष फजी निष्कर्ष

एक फजी निष्कर्ष एक प्रक्रिया के रूप में समझा जाता है जिसमें कुछ परिणाम, संभवतः फजी भी होते हैं, फजी परिसर से प्राप्त होते हैं। अनुमानित तर्क किसी व्यक्ति की प्राकृतिक भाषा को समझने, लिखावट को समझने, ऐसे खेल खेलने की क्षमता को कम करता है, जिसके लिए मानसिक प्रयास की आवश्यकता होती है, सामान्य रूप से, जटिल और अपूर्ण परिभाषित वातावरण में निर्णय लेते हैं। गुणात्मक, गलत शब्दों में तर्क करने की यह क्षमता मानव बुद्धि को कंप्यूटर की बुद्धिमत्ता से अलग करती है।



पारंपरिक तर्क में अनुमान का मूल नियम, मोडस पॉन्सेंस नियम है, जिसके अनुसार हम कथन B की सत्यता को A और A -> B के सत्य से आंकते हैं, उदाहरण के लिए, यदि A का कथन है कि "Stepan एक अंतरिक्ष यात्री है," B वह कथन है "Stepan अंतरिक्ष में उड़ता है" , तब यदि कथन "स्टीफन एक अंतरिक्ष यात्री है" और "यदि स्टीफन एक अंतरिक्ष यात्री है, तो वह अंतरिक्ष में उड़ जाता है," "स्टीफन अंतरिक्ष में उड़ता है" यह कथन सत्य है।



हालांकि, पारंपरिक तर्क के विपरीत, फजी लॉजिक का मुख्य उपकरण मोडस पॉन्सन नियम नहीं है, लेकिन तथाकथित कंपोजिशन इंट्रेंस नियम, एक बहुत ही विशेष मामला है जो मॉडस पॉन्सन नियम है।



मान लीजिए कि एक वक्र y = f (x) है और एक मान x = a दिया गया है। फिर इस तथ्य से कि y = f (x) और x = a, हम उस y = b = f (a) का निष्कर्ष निकाल सकते हैं।



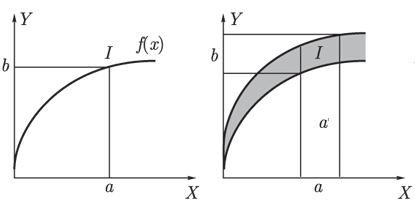
अब हम इस प्रक्रिया को सामान्य करते हैं, यह मानते हुए कि एक अंतराल है और एफ (x) एक फ़ंक्शन है जिसके मान अंतराल हैं। इस स्थिति में, अंतराल a = b को अंतराल a के अनुसार खोजने के लिए, हम पहले सेट को 'a' बेस के साथ बनाते हैं और इसके अंतरंग I को वक्र के साथ पाते हैं जिनके मान अंतराल हैं। तब हम ओए अक्ष पर इस चौराहे को प्रोजेक्ट करते हैं और अंतराल बी के रूप में वाई का वांछित मूल्य प्राप्त करते हैं। इस प्रकार, इस तथ्य से कि y = f (x) और x = A ओएक्स अक्ष का एक फ़ज़ी सब्मिट है, हमें ओए अक्ष के फ़ज़ी सबसेट बी के रूप में y का मान मिलता है।



यू और वी को क्रमशः बेस चर यू और वी के साथ दो सार्वभौमिक सेट होने दें। A और F सेट U और U x V के फ़र्ज़ी सबसेट होते हैं। फिर इंफ़ेक्शन के कंपोज़िशन नियम में कहा गया है कि फ़ज़ी सेट A और F सेट करता है।



आज्ञा देना A और B फ़र्ज़ी कथन हैं और m (A), m (B) संबंधित सदस्यता कार्य हैं। तब निहितार्थ A -> B कुछ सदस्यता फ़ंक्शन m (A -> B) के अनुरूप होगा। पारंपरिक तर्क के अनुरूप, हम यह मान सकते हैं



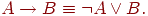
तो



हालांकि, यह निहितार्थ ऑपरेटर का एकमात्र सामान्यीकरण नहीं है, अन्य हैं।

कार्यान्वयन

प्रत्यक्ष फजी इंजेक्शन विधि को लागू करने के लिए, हमें निहितार्थ ऑपरेटर और टी-मानदंड चुनने की आवश्यकता है।

प्रारंभिक T- मान न्यूनतम कार्य है:

1. def t_norm (v1, v2): return min (v1, v2)
   
   
   
   
2. def t_norm (v1, v2): return min (v1, v2)
   
   
   
   

और Gödel फ़ंक्शन निहितार्थ ऑपरेटर होगा:

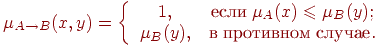
1. डीईएफ इंप्लांट (v1, वी 2):
2. '' ' <br/> Godel निहितार्थ <br/> ' '' ''
3. अगर v1 <= v2:
4. वापसी 1 । 0
5. और :
6. वापसी v2

इनपुट डेटा में ज्ञान (अस्पष्ट सेट) और नियम (निहितार्थ) शामिल होंगे, उदाहरण के लिए:

A = {(X1, 0.0), (x2, 0.2), (x3, 0.7), (x4, 1.0)}।

B = {(X1, 0.7), (x2, 0.4), (x3, 1.0), (x4, 0.1)}।

ए => बी।



निहितार्थ कार्टेशियन मैट्रिक्स के रूप में प्रस्तुत किया जाएगा, जिनमें से प्रत्येक तत्व की गणना चयनित निहितार्थ ऑपरेटर (इस उदाहरण में, गोडेल फ़ंक्शन) का उपयोग करके की जाती है:

1. def Comp__pl (set1, set2):
2. '' ' <br/> कम्प्यूटिंग निहितार्थ <br/> ' '' ''
3. संबंध = {}
4. i में set1.items () के लिए:
5. संबंध [i] = {}
6. j में set2.items () के लिए:
7. v1 = set1.value (i)
8. v2 = set2.value (j)
9. संबंध [i] [जे] = निहित (v1, वी २)
10. सम्बन्ध लौटाओ

उपरोक्त डेटा के लिए यह होगा:

निष्कर्ष:

ए => बी।

एक्स 1 एक्स 2 एक्स 3 एक्स 4

X1 1.0 1.0 1.0 1.0

x2 1.0 1.0 1.0 0.1

x3 1.0 0.4 1.0 0.1

x4 0.7 0.4 1.0 0.1



इसके अलावा, आउटपुट के परिणामस्वरूप, एक नया सेट प्राप्त होता है:

1. डीईएल निष्कर्ष (सेट, रिलेशन):
2. '' ' <br/> निष्कर्ष <br/> ' ''
3. conl_set = []
4. मैं संबंध में:
5. l = []
6. j के लिए संबंध में [i]:
7. v_set = set .value (i)
8. v_impl = संबंध [i] [j]
9. l.append (t_norm (v_set, v_impl))
10. मान = अधिकतम (l)
11. conl_set.append ((i, value))
12. वापसी conl_set

परिणाम:

B '= {(X1, 1.0), (x2, 0.7), (x3, 1.0), (x4, 0.7)}।

सूत्रों का कहना है

• रुतकोवस्काया डी।, पिलिंस्की एम।, रुतकोवस्की एल। तंत्रिका नेटवर्क, आनुवंशिक एल्गोरिदम और फजी सिस्टम: प्रति। पॉलिश से। आई। डी। रुडिंस्की। - एम ।: हॉट लाइन - टेलीकॉम, 2006 ।-- 452 पी .: बीमार।
• ज़ैध ला फ़ज़ी सेट्स, सूचना और नियंत्रण, 1965, वॉल्यूम। 8, एस। 338-353