समान प्राथमिकताओं वाले लोगों की खोज करने के लिए टैनिमोटो गुणांक का उपयोग करना

"सामूहिक मन की प्रोग्रामिंग" के लिए अभ्यासों को हल करते हुए, मैंने इस पुस्तक में वर्णित एल्गोरिदम में से एक के कार्यान्वयन को साझा करने का निर्णय लिया (अध्याय 2 - व्यायाम 1)।



प्रारंभिक शर्तें इस प्रकार हैं: मान लें कि हमारे पास महत्वपूर्ण रेटिंग वाला एक शब्दकोश है:

आलोचक = { 'लिसा रोज़' : { 'सुपरमैन रिटर्न्स' : 3.5 , 'यू, मी और डुप्री' : 2.5 , 'द नाइट लिसनर' : 3.0 }

'जीन सीमोर' : { 'सुपरमैन रिटर्न्स' : 5.0 , 'द नाइट लिसनर' : 3.5 , 'यू, मी और डुप्री' : 3.5 } }

जितना ज्यादा स्कोर होगा, उतना ही ज्यादा आपको फिल्म पसंद आएगी।

यह गणना करना आवश्यक है: क्रम में आलोचकों के हित कितने समान हैं, उदाहरण के लिए, एक की रेटिंग के आधार पर दूसरे को फिल्मों की सिफारिश करने में सक्षम होने के लिए?







गुणांक तनीमोतो - दो सेटों की समानता की डिग्री का वर्णन करता है। इंटरनेट पर, मुझे इसकी गणना करने के सूत्र के लिए कई विकल्प मिले। और मैंने निम्नलिखित पर ध्यान देना चाहा:



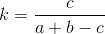
जहाँ k तनीमोतो गुणांक है (0 से 1 तक की संख्या), यह 1 के करीब है, सेट के समान है;

ए पहले सेट में तत्वों की संख्या है;

b दूसरे सेट में तत्वों की संख्या है;

सी दो सेटों में आम तत्वों की संख्या है;

अब हमें दो आलोचकों की रेटिंग की तुलना करने की आवश्यकता है।

बस एक बिंदु स्पष्ट करना चाहता हूं। हमारे दो सेटों में एक सामान्य तत्व क्या माना जाना चाहिए? यह स्पष्ट है कि मूल्यांकन को अपने वर्तमान रूप में प्रस्तुत करने से समान हितों वाले लोगों की सही पहचान नहीं होगी। दरअसल, संक्षेप में, इस एल्गोरिथ्म के लिए 3.5 और 4.0 की समान रेटिंग पूरी तरह से अलग-अलग संख्याएं हैं। इसलिए, मेरी राय में, टैनिमोटो गुणांक का उपयोग किया जाना चाहिए, यदि रेटिंग विकल्पों की संख्या 2-3 से अधिक नहीं है (उदाहरण के लिए, "मुझे यह पसंद आया, मुझे यह पसंद नहीं आया," या "मैं यह सलाह देता हूं, मैंने इसे नहीं देखा, मैं इसकी अनुशंसा नहीं करता हूं") मैंने अधिक सुविधाजनक काम के लिए शब्दकोश को थोड़ा बदलने का फैसला किया। रेटिंग में निम्नलिखित परिवर्तन को लागू किया: यदि रेटिंग 3 से कम है, तो फिल्म पसंद नहीं की गई थी (रेटिंग बन जाती है - 0), अन्यथा इसे पसंद किया गया (रेटिंग बन जाती है - 1)। इस रूप में डेटा हमारे प्रयोग के लिए अधिक उपयुक्त हैं।

def_for_tanimoto को हराया ( आलोचक_छूट ) :

arr = critics_arr। कॉपी ( )

गिरफ्तारी में आलोचक के लिए :

गिरफ्तारी में फिल्म के लिए [ समीक्षक ] :

अगर गिरफ्तार [ आलोचक ] [ फिल्म ] < 3 :

गिरफ्तार [ आलोचक ] [ फिल्म ] = ०

और :

गिरफ्तार [ आलोचक ] [ फिल्म ] = १

वापसी गिरफ्तार

आउटपुट में हमें निम्नलिखित शब्दकोश मिलता है:

आलोचक = { 'लिसा रोज़' : { 'सुपरमैन रिटर्न्स' : 1 , 'यू, मी और डुप्री' : 0 , 'द नाइट लिसनर' : 1 }

'जीन सीमोर' : { 'सुपरमैन रिटर्न्स' : 1 , 'द नाइट लिसनर' : 1 , 'यू, मी और डुप्री' : 1 } }

और फिर हम एक फ़ंक्शन लिखते हैं जो दो आलोचकों की रेटिंग के समानता गुणांक की गणना करता है।

डी टी टान्मोटो ( क्रिटिक्स_रियर, आलोचक 1, आलोचक 2 ) :

गिरफ्तारी = ready_for_tanimoto ( आलोचक_कार्य )



a = len ( गिरफ्तार [ आलोचक ]] )

बी = लेन ( गिरफ्तार [ आलोचक 2 ] )

सी = 0.0



गिरफ्तारी में फिल्म के लिए [ समीक्षक 1 ] :

अगर गिरफ्तारी [ समीक्षक ] [ फिल्म ] == गिरफ्तार [ आलोचक 2 ] [ फिल्म ] :

c = c + 1



koef = c / ( a + b - c )

वापसी koef

Tanimoto फ़ंक्शन की कार्यक्षमता की जाँच करें।



>>> प्रिंट टेंमोतो (आलोचक, 'जीन सीमोर', 'लिसा रोज')

>>> 0.5



मेरी राय में, परिणाम सही है। यह ध्यान दिया जाना चाहिए कि प्रत्येक आलोचक के लिए रेटिंग की संख्या में वृद्धि के साथ, समानता गुणांक की गणना करने की सटीकता बढ़ जाएगी।



यदि हमारे पास आकलन का एक डेटाबेस होता है, तो लोगों के हितों की समानता के गुणांक की गणना करना और टैनिमोटो विधि पर सिफारिशें देना शुरू करना संभव होगा।



आप यहां उदाहरण पाठ डाउनलोड कर सकते हैं ।

आप लेखक की वेबसाइट पर पुस्तक से सभी उदाहरणों का पूरा पाठ डाउनलोड कर सकते हैं। वहाँ आप महत्वपूर्ण रेटिंग के साथ एक और अधिक पूर्ण सरणी पा सकते हैं।