
A small module for working with arrays in Python without using third-party libraries (a NumPy clone, but only in pure Python).
The homework at the university was asked to write a program that calculates the norms and decompositions of the matrix, but was forbidden to use third-party libraries. The choice of programming language is not limited. I chose python (which was a mistake, because it is much slower than Java and C / C ++) and accordingly I cannot use NumPy. In the process, I had to write functions for performing operations with arrays, functions for finding minors, determinants, etc. The result is a mini library for working with arrays.
My pure python code is much slower than NumPy, which does C and Fortran calculations (plus my code is not optimized).
What can MatLOL:
- Sum, difference and product of matrices
- Matrix product by number
- Matrix Transpose
- Minor matrix
- Matrix determinant
- inverse matrix
- Union matrix
- Matrix condition number
- The first, second (not finalized), Euclidean and infinite matrix norms
- Solution of the equation AX = B
- LU decomposition
- Cholesky decomposition
- Seidel Method
MathLOL Examples
Import the module:
# from mathlol import * from mathlol import mathlol
Matrix initialization
matrix = mathlol() matrix.set([[1, 2, 3], [4, 5, 6], [7, -8, 9]]) matrix.get() #
Some matrix operations
matrix * 2 # 2 A = [[0, 0, 0], [0, 1, 0], [0, 0, 0]] # 2 matrix.dot(A) matrix * A matrix.transposition() # matrix.minor(i = 0, j = 0) # matrix.determinant() # matrix.inverse() # L, U = matrix.lu() # LU matrix.seidel(b = [[5.0], [9.0], [1.0]]) #
There are also functions for working with vectors
vector = mathlol() vector.set([1, 2, 3, 4, 5]) vector.checkvector() # , vector.norm1_vector() vector.norm2_vector() vector.norm3_vector()
Other examples
MathLOL Performance
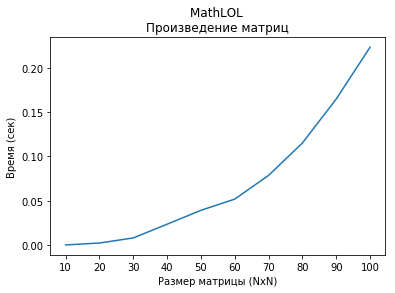
Let's see the speed of computing products of matrices of size NxN. Matrices are filled with random integers from -100 to 100.
The code
from mathlol import mathlol import time import random import matplotlib.pyplot as plt # data = {} for i in range(10, 110, 10): array = [] for i_ in range(i): temp = [] for j_ in range(i): temp.append(random.randint(-100, 100)) array.append(temp) data[i] = array # mlol_dot = {} for key in data.keys(): matrix = mathlol() matrix.set(matrix = data[key]) start = time.process_time() result = matrix * matrix end = time.process_time() - start mlol_dot[key] = end # plt.plot(mlol_dot.keys(), mlol_dot.values()) plt.title("MathLOL \n ") plt.xlabel(" (NxN)") plt.ylabel(" ()")
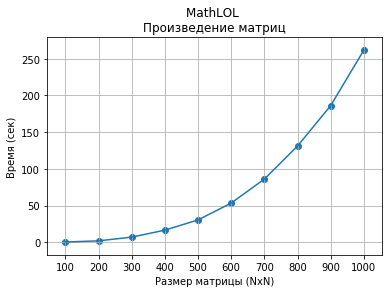
The speed of computing matrix products from 100x100 to 1000x1000
Compare the computational speed of numpy and mathlol. Unfortunately, mathlol was very slow in speed and I decided to take matrices for sizes from 100x100 to 1000x1000 for numpy, and for mathlol from 10x10 to 100x100.
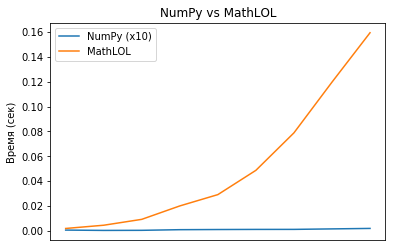
MathLOL calculated the product of the matrix 100x100 by itself in 0.16 seconds, and NumPy calculated the product of the matrix 1000x1000 by itself in 0.002 (!!!) seconds. The difference is huge.
Our task was simply to implement various functions for working with matrices, which we did, but the program with large matrices does not work as fast as we would like. It remains to refine the program, add a few more functions (for example, a function for calculating the Todd number), I would be grateful if you look at the code, point out errors, and perhaps help refine the code.
That's all, the code and examples are posted on the github .
PS In the process of writing this article, I wanted to experiment and build C / C ++ into my module. I’ll deal with this in the near future and see how close it will be to NumPy’s performance.