
Original translation in my blog
How did this book get to me?
In May 2017, I received an email from my old high school teacher named George Rutter, in which he wrote: “ I have a copy of the big German Dirac book (Die Prinzipien der Quantenmechanik), which belonged to Alan Turing, and thereafter as I read your book Idea Makers , it seemed to me for granted that you are the person who needs it . " He explained to me that he had received a book from another (by that time deceased) my school teacher Norman Rutledge , about whom I knew that he was a friend of Alan Turing. George concluded his letter with the phrase: “ If you need this book, I could hand it to you the next time you come to England .”
After a couple of years in March 2019, I really arrived in England, after which I agreed with George to meet for breakfast at a small hotel in Oxford. We ate, chatted and waited for the food to settle. Then came the right moment to discuss the book. George put his hand in his briefcase and pulled out a rather modestly designed, typical academic volume of the mid-1900s.

I opened the cover, wondering if it could be on the back of the inscription: " Alan Turing 's Property" or something like that. But, unfortunately, this was not the case. Nevertheless, a sufficiently expressive note on four sheets from Norman Rutledge to George Rutter, written in 2002, was attached to it.
I knew Norman Rutledge when I was still a high school student at Eton in the early 1970s. He was a math teacher nicknamed The Nutty Norman. He was a pleasant teacher in all respects and told endless stories about mathematics and all sorts of other interesting things. He was responsible for ensuring that the school received a computer (programmed with a punched tape the width of a desk) - this was the very first computer I had ever used .
In those days, I did not know anything about Norman's past (remember that this was long before the advent of the Internet). I only knew that he was "Dr. Rutledge." He often told stories about people from Cambridge, but in his stories he never mentioned Alan Turing. Of course, Turing was not famous enough then (although, as it turns out, I already heard about him from someone who knew him in Bletchley Park (the mansion in which the encryption center was located during World War II)).
Alan Turing was not famous until 1981, when I first began to study simple programs , although back then in the context of cellular automata, and not Turing machines .
Suddenly, one day, looking at a catalog of cards in the library of the California Institute of Technology , I stumbled upon a book , Alan M. Turing , written by his mother Sarah Turing. The book had a lot of information, including about Turing's unpublished scientific works on biology. However, I did not learn anything about his relationship with Norman Rutledge, since the book did not mention anything about him (although, as I found out, Sarah Turing corresponded with Norman about this book , and Norman even wrote a review of it in the end).

Ten years later, tuned with extreme curiosity for Turing and his (then unpublished) biology work , I visited the Turing archive at King's College, Cambridge . Soon, having familiarized myself with what they had from Turing's work, and having spent some time on it, I thought that at the same time I could ask him to see his personal correspondence as well. Looking through it, I found several letters from Alan Turing to Norman Rutledge.
By that time, the biography of Andrew Hodges was published, which did so much so that Turing finally became famous, it confirmed that Alan Turing and Norman Rutledge were really friends, and also that Turing was a scientific consultant to Norman. I wanted to ask Rutledge about Turing, but by then Norman was already retired and led a secluded life. Nevertheless, when I completed work on the book A New Kind of Science in 2002 (after my ten-year retreat), I tracked it down and sent him a copy of the book with the caption, “To My Last Math Teacher.” Then we corresponded a little, and in 2005 I again came to England and agreed to meet with Norman for a cup of tea in a luxury hotel in central London.
We had a nice talk about many things, including Alan Turing. Norman began our conversation with the story that he really knew Turing, for the most part superficially, 50 years ago. But still he had something to tell about him personally: " He was unsociable ." " He giggled a lot ." " He could not really speak with nemathematics ." " He was always afraid to upset his mother ." " He left during the day and ran a marathon ." " He was not too ambitious ." Then the conversation returned to Norman's identity. He said that despite the fact that he had already retired for 16 years, he still writes articles for the Mathematical Newspaper , so that, in his words, “to complete all his scientific work before moving to another world ” , where, as he added with a barely perceptible smile, " all mathematical truths will certainly be revealed ." When the tea party was over, Norman put on his leather jacket and headed for his moped, completely ignoring the explosions that disrupted traffic in London that day.
This was the last time I saw Norman, he died in 2013.
Six years later, I sat at breakfast with George Ratter. With me was a note from Rutledge, written by him in 2002 in his characteristic handwriting:

At first I read the note fluently. She was expressive as usual:
I received a book by Alan Turing from his friend and executor Robin Gandy (at King's College it was normal to give out books from the collection of deceased comrades, and I chose the collection of poems by A.E. Houseman from Ivor Ramsey 's books as a suitable gift (he was the dean and jumped from the chapel [in 1956]) ...
Later in a short note he writes:
You ask where, in the end, this book should have got - in my opinion, it should go to someone who appreciates everything related to Turing's work, so its fate depends on you.
Stephen Wolfram sent me his impressive book, but I didn’t dive deep enough into it ...
In conclusion, he congratulated George Ratter on having the courage to move (as it turned out, temporarily) to Australia after retiring, saying that he himself would " play moving to Sri Lanka as an example of a cheap and lotus-like existence, " but added that “the events taking place there now indicate that he should not have done this ” (apparently referring to the civil war in Sri Lanka).
So what is hidden in the bowels of the book?
So, what have I done with a copy of a German-language book written by Paul Dirac that once belonged to Alan Turing. I do not read German, but I had a copy of the same book in English (which is the language of its original) of the 1970s edition. However, one day at breakfast it seemed to me correct that I should carefully review the book page by page. In the end, this is a common practice when dealing with antique books.
It should be noted that I was struck by the elegance of Dirac's presentation. The book was published in 1931, but its pure formalism (and, yes, despite the language barrier, I could read the mathematics described in the book) is almost the same as if it was written today. (I don’t want to focus too much on Dirac here, but my friend Richard Feynman told me that, at least in his opinion, Dirac’s exposition is monosyllabic. Norman Rutledge told me that he was friends in Cambridge with Dirac’s adoptive son , who became a theorist in Norman was quite often in Dirac’s house and said that the “great man” sometimes personally faded into the background, while the foreground always had a lot of mathematical puzzles. Unfortunately, I myself have never met Paul Dirac, although I was told that after t wow, as he finally left Cambridge and went to Florida, he lost most of his former stiffness and became quite a sociable person).
But back to the book of Dirac, which belonged to Turing. On page 9, I noticed underlines and small margin notes written in simple pencil. I continued to flip pages. After several chapters, the notes disappeared. But then, all of a sudden, I found a note embedded in page 127 with the following content:
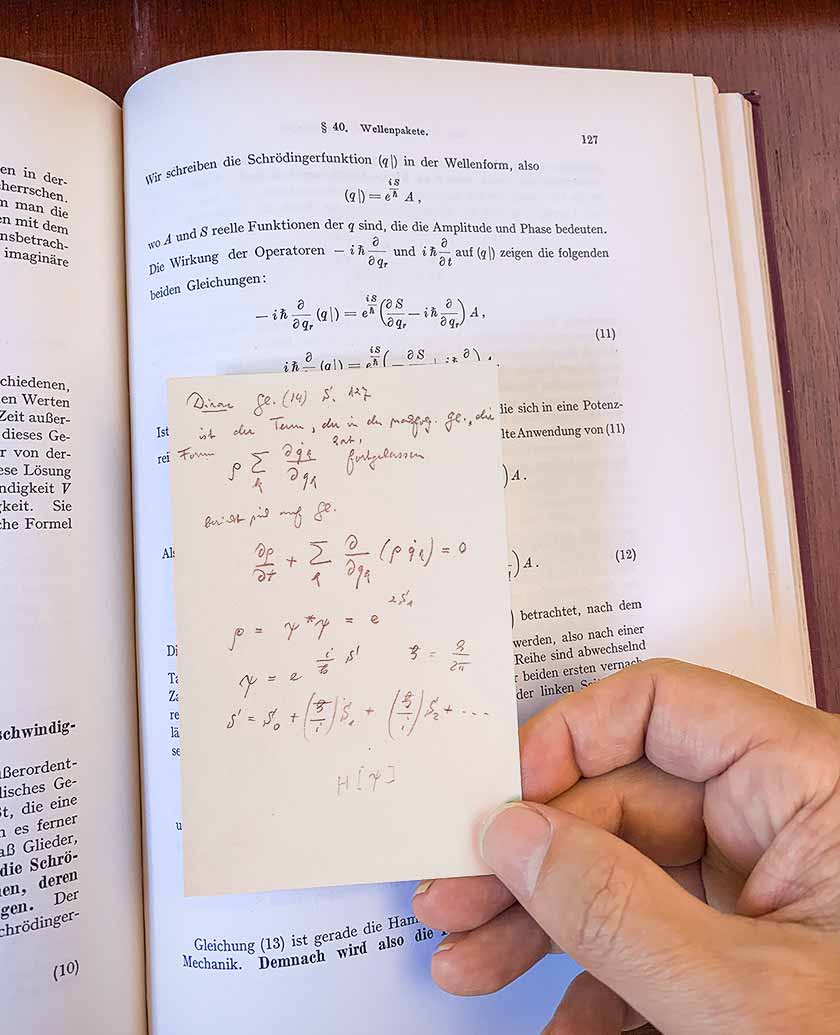
It was written in German in standard German handwriting. And it looks like it could somehow be connected with Lagrangian mechanics . I thought that probably someone owned this book before Turing, and this must be a note written by this person.
I continued to leaf through the book. No notes. And I thought that I could no longer find anything. But then, on page 231, I found a company bookmark with printed text:

Will I eventually find anything else? I continued to leaf through the book. Then, at the end of the book, on page 259, in the section on the relativistic theory of electrons, I found the following:

I unfolded this sheet of paper:
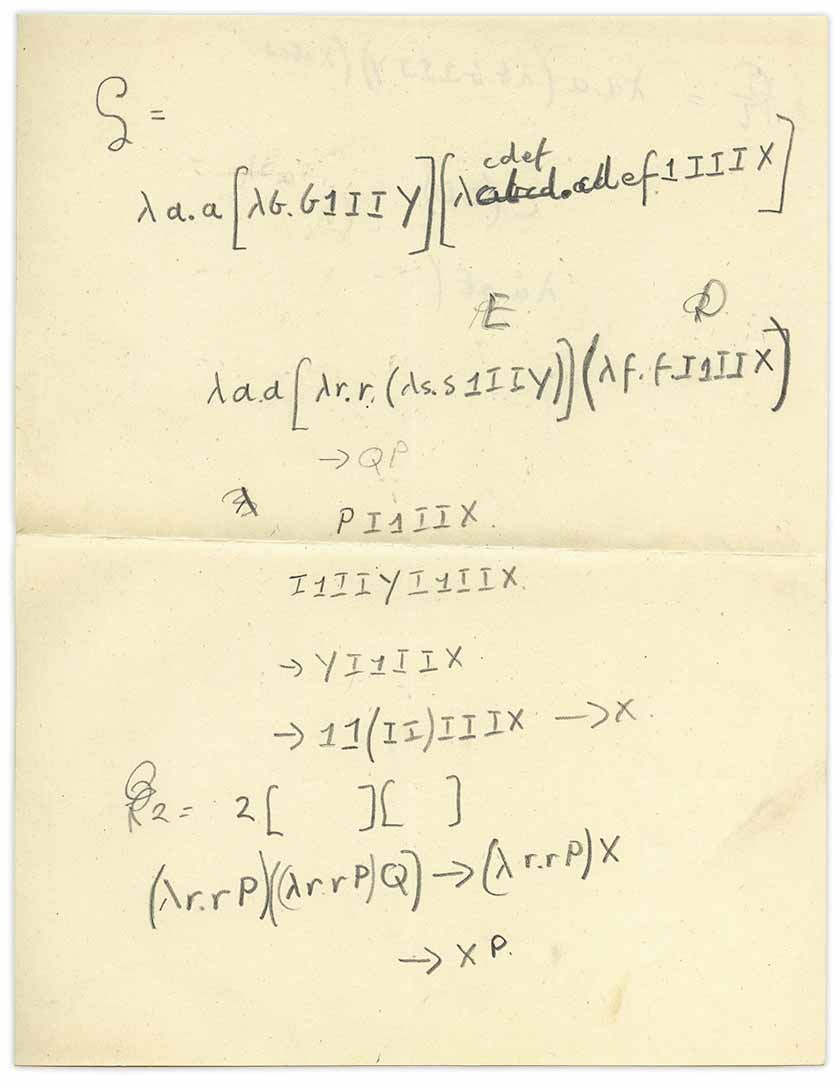
I immediately realized that this was a lambda calculus with an admixture of combinators , but how did this sheet appear here? Recall that this book is a book on quantum mechanics, but the enclosed sheet deals with mathematical logic, or what is now called the theory of computation. This is typical of Turing's writings. I wondered if Turing personally wrote this note.
Even during breakfast, I searched the Internet for Turing's handwriting samples, but did not find examples in the form of calculations, so I could not draw conclusions about the exact identity of the handwriting. And soon I had to go. I carefully packed the book, ready to reveal the secret of what the page was and who wrote it, and took it with me.
About the book
First of all, let's discuss the book itself. The Principles of Quantum Mechanics by Paul Dirac was published in English in 1930 and was soon translated into German. (Dirac's preface is dated May 29, 1930; it belongs to the translator, Werner Bloch , on August 15, 1930.) The book became a milestone in the development of quantum mechanics, systematically establishing a clear formalism for performing calculations, and, among other things, explaining Dirac’s prediction about the positron , which will be opened in 1932.
Why did Alan Turing have a book in German, not English? I do not know this for sure, but in those days German was the leading language of science, and we know that Alan Turing was able to read it. (After all, in the title of his famous Turing machine work “ About computable numbers with an appendix to the Resolution Problem (Entscheidungsproblem) ”was a very long German word - and in the main part of the article he operates with rather obscure Gothic characters in the form of“ German letters ”, which he used instead of, for example, Greek characters).
Alan Turing bought this book himself or handed it to him? I dont know. On the inside of the cover of Turing's book there is a pencil notation “20 / -”, which was the standard notation “20 shillings”, similar to £ 1. On the right page there is an erased “26.9.30”, supposedly meaning September 26, 1930 - perhaps the date the book was first purchased. Then, in the far right corner, the erased number is "20". Perhaps this is again the price. (Could this be the price in the Reichsmarks , if we assume that the book was sold in Germany? At that time, 1 Reichsmark was worth about 1 shilling, the German price would probably be written like, for example, “20 RM”.) Finally, on the inside of the back cover is “c 5 / -” - maybe it’s (with a big discount) the price for a used book.
Let's look at the main dates of Alan Turing's life. Alan Turing was born on June 23, 1912 (coincidentally, exactly 76 years before Mathematica 1.0 ). In the fall of 1931, he entered King's College, Cambridge. He received his bachelor's degree after the standard three years of study, in 1934.
In the 1920s and early 1930s, quantum mechanics was a hot topic, and Alan Turing was certainly interested in it. We know from his archives that in 1932, as soon as the book was published, he received the " Mathematical Foundations of Quantum Mechanics " by John von Neumann (in German ). We also know that in 1935 Turing received a task from the Cambridge physicist Ralph Fowler on the subject of the study of quantum mechanics. (Fowler suggested calculating the dielectric constant of water , which is actually a very difficult task, requiring a full analysis with the interacting quantum field theory, which is still not completely solved).
And yet, when and how did Turing get his copy of Dirac's book? Given that the book has a broken price, Turing allegedly bought it already used. Who was the first owner of the book? The notes in the book seem to relate primarily to the logical structure, it is noted that some logical relationship should be considered an axiom. Then what about the note attached on page 127?
Well, this may be a coincidence, but on page 127, Dirac talks about the quantum principle of least action and lays the foundation for an integral along the Feynman path - which is the basis of all modern quantum formalism. What does the note contain? It contains an extension of equation 14, which is an equation for the temporal evolution of quantum amplitude. The author of the note replaced Dirac A for amplitude with ρ, possibly reflecting the earlier German (analogy of liquid density) German record. Then the author tries to expand the action in powers of ℏ (the Planck constant divided by 2π, which is sometimes called the Dirac constant ).
But it seems that from what is contained on the page, there is little that can be learned useful. If you keep the page in the light, it contains a small surprise - a watermark with the inscription "Z f. Physik. Chem. B ”:

This is an abridged version of Zeitschrift für physikalische Chemie, Abteilung B , the German journal of physical chemistry, which has been published since 1928. Perhaps the note was written by the journal editor? Here is the title of the magazine for 1933. Conveniently, the editors are listed with their location, and one of them stands out: “Born · Cambridge”.

This is Max Bourne who is the author of the Bourne rule and much more in the theory of quantum mechanics (as well as the grandfather of singer Olivia Newton-John ). So, this note may have been written by Max Born? But, unfortunately, this is not so, because the handwriting does not match.
What about the bookmarks on page 231? Here it is from two sides:

The bookmark is weird and pretty pretty. But when was it made? There is a Heffers bookstore in Cambridge , although it is now part of Blackwell. For more than 70 years (until 1970), Heffers was located at the address, as the bookmark shows, 3 and 4 by Petty Cury .
This tab contains an important key - this is the phone number „Tel. 862. " It turned out that in 1939 most of Cambridge (including Heffers) switched to four-digit numbers, and, of course, by 1940 bookmarks were printed with "modern" phone numbers. (The English phone numbers gradually grew longer; when I grew up in England in the 1960s, our phone numbers were Oxford 56186 and Kidmore End 2378. In part, I remember these numbers because, oddly enough, it’s now it didn’t look, I always called my number when answering an incoming call).
The bookmark in this form was printed until 1939. But how long before that? You can find quite a few scans of old Heffers advertisements on the Internet, at least since 1912 (along with “We ask you to satisfy your requests ...”) they add “Phone 862”, adding “(2 lines)”. There are also some bookmarks with similar design that can be found in books since 1904 (although it is unclear whether they were original for these books (that is, printed at the same time). For the purposes of our investigation, it seems we can conclude that this book came from the Heffers store (which, incidentally, was the main bookstore in Cambridge) sometime between 1930 and 1939.
Page with lambda calculus
So now we know something about when the book was bought. But what about the “lambda calculus page”? When was this written? Well, of course, by then, lambda calculus should have been invented. And this was done by Alonzo Church , a mathematician from Princeton , in its original form in 1932 and in its final form in 1935. (There were works by scientists of their predecessors, but they did not use the notation λ).
There is a complex relationship between Alan Turing and lambda calculus. In 1935, Turing became interested in the "mechanization" of mathematical operations, and invented the idea of a Turing machine using it to solve problems in the foundations of mathematics. Turing sent an article on this subject to the French magazine ( Comptes rendus ), but it was lost in the mail; and then it turned out that the addressee to whom he sent it was still not there, since he had moved China.
But in May 1936, even before Turing could send his article elsewhere, the work of Alonzo Church arrived from the United States . Turing had already complained that when he developed the proof of the central limit theorem in 1934, he discovered that there was a Norwegian mathematician who had already presented the proof in 1922.
It is easy to understand that Turing machines and lambda calculus are actually equivalent in the types of calculations that they can represent (and this is the beginning of Church-Turing thesis ). However, Turing (and his teacher Max Newman ) were convinced that Turing's approach was excellent enough to merit a separate publication. In November 1936 (and with corrected typos the following month), the famous Turing article “On Computable Numbers ...” was published in the works of the London Mathematical Society .
To fill up the timeline a little: from September 1936 to July 1938 (with a break of three months in the summer of 1937) Turing was in Princeton, having gone there, with the aim of becoming a graduate student of Alonzo Church. During this period at Princeton, Turing apparently concentrated entirely on mathematical logic - he wrote several difficult to read articles full of Church's lambda calculus - and most likely he did not have a book on quantum mechanics with him.
Turing returned to Cambridge in July 1938, but by September of that year he was part-time at the Government School of Codes and Ciphers , and a year later he moved to Bletchley Park, with the goal of working full-time there on issues related to cryptanalysis . After the war ended in 1945, Turing moved to London in order to work at the National Physical Laboratory to develop a computer project. He spent the 1947–8 school year in Cambridge, but then moved to Manchester in order to develop the first computer there .
In 1951, Turing began to seriously engage in theoretical biology . (For me personally, this fact is somewhat ironic, because it seems to me that Turing always subconsciously believed that biological systems should be modeled by differential equations, and not something discrete, like Turing machines or cellular automata). He also turned his interest in physics again, and by 1954 he even wrote to his friend and student Robin Gandy that: “ I tried to invent new quantum mechanics ” (although he added: “ but it’s not really a fact that will work out ”). But, unfortunately, everything suddenly broke off on June 7, 1954, when Turing suddenly died. (I suppose this was not suicide, but that is a completely different story.)
So, back to the lambda calculus page. Bring it to the light, and again see the watermark:

It can be seen that this is a piece of paper of British manufacture, and it seems unlikely to be used in Princeton. But can we accurately date it? Well, with some help from the British Association of Historic Paper Manufacturers , we know that the official paper producers were Spalding & Hodge, Papermakers, Drury House wholesale and export companies, Russell Street in Drury Lane, Covent Garden, London. This may help us, but not very much, since it can be assumed that their Excelsior paper brand seems to have been included in the supply catalogs from the 1890s to 1954.
What does this page say?

So, let's take a closer look at what is on both sides of the leaf. Let's start with lambdas.
Here is a way to define “pure” or “anonymous” functions , and they are the basic concept in mathematical logic, and now in functional programming. These functions are quite common in the Wolfram Language , and their job is pretty easy to explain. For example, someone writes f [ x ] to denote the function f applied to the argument x. And there are many named f functions such as Abs or Sin or Blur . But what if someone wants f [ x ] to be 2x +1 ? There is no immediate name for this function. But is there another form of assignment, f [ x ]?
The answer is yes: instead of f we write
Function[a,2a+1]
. And in the Wolfram
Function [a,2a+1][x]
language
Function [a,2a+1][x]
applies functions to the argument x, yielding
2x+1
as a result.
Function[a,2a+1]
is a “pure” or “anonymous” function, which is a pure operation of multiplying by 2 and adding 1.
So, λ in the lambda calculus is an exact analogue of Function in the Wolfram Language - and therefore, for example, λ a. (2 a + 1) is equivalent to
Function[a, 2a + 1]
. (It is worth noting that the function, say,
Function[b,2b+1]
equivalent; the “related variables” a or b are just places for substituting the argument of the function - and in Wolfram Language they can be avoided using alternative options for defining a pure function
(2# +1)&
).
In traditional mathematics, functions are usually considered as objects that display input data (e.g., integers) and output data (which are also, for example, integers). But what is this Function object (or λ)? In essence, this is a structural operator that takes expressions and turns them into functions. This may seem a little strange in terms of traditional mathematics and the mathematical form of writing, but if someone needs to manipulate arbitrary characters, which is much more natural, even if at first it seems a bit abstract. (It should be noted that when users learn the Wolfram Language, I can always say that they have overcome a certain threshold of abstract thinking when they get an idea of Function ).
Lambdas are just part of what's on the page. There is another, even more abstract concept - these are combinators . Consider the rather obscure
PI1IIx
line? What does that mean? In fact, this is a sequence of combinators, or, some abstract composition of symbolic functions.
The usual superposition of functions, quite familiar in mathematics, in the Wolfram Language can be written in the form:
f[g[x]]
- which means “apply f to the result of applying g to x ”. But are brackets really needed for this? In Wolfram,
f@g@ x
is an alternative form of notation. In this entry, we rely on the Wolfram Language definition: the @ operator is associated with the right-hand side, so
f@g@x
equivalent to
f@(g@x)
.
But what will the entry
(f@g)@x
mean? This is equivalent to
f[g][x]
. And if f and g were ordinary functions in mathematics, this would be pointless, but if f is a higher-order function , then
f[g]
itself can be a function that can very well be applied to x .
Note here there is still some complexity. In
f[]
- f is a function of one argument. And
f[]
equivalent to writing
Function[a, f[a]][x]
. But what about the function of two arguments, say,
f[x,y]
? This can be written as
Function[{a,b},f[a, b]][x, y]
. But what about
Function[{a},f[a,b]]
? What is it? There is a "free variable" b , which is simply passed to the function.
Function[{b},Function[{a},f[a,b]]]
will bind this variable, and then
Function[{b},Function[{a},f [a, b]]][y][x]
gives
f[x,y]
again. (Setting the function so that it has one argument is called "currying" in honor of the scientist logician named Haskell Curry ).
If there are free variables, then there are many different complexities as to how functions can be defined, but if we restrict ourselves to Function or λ objects that do not have free variables, then they can basically be set freely. Such objects are called combinators.
Combinators have a long history. It is known that they were first proposed in 1920 by David Gilbert's disciple, Moses Schoenfinkel .
At that time, only very recently it was discovered that it was not necessary to use And , Or and Not expressions to represent expressions in the standard propositional logic: it was enough to use the only operator, which we will now call Nand (because, for example, if we write Nand as ·, Then
Or[a,b]
takes the form (a · a) · (b · b) ). Schönfinkel wanted to find the same minimal representation of predicate logic, or essentially logic, including functions.
He came up with two “combinators” S and K. In the Wolfram Language, this is written as
K [x _] [y_] → x and S [x _] [y _] [z_] → x [z] [y [z]].
It is noteworthy that it was possible to use these two combinators to perform any calculations. For example,
S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]
can be used as a function to add two integers.
All these, to put it mildly, are rather abstract objects, but now that we understand what Turing machines and lambda calculus are, we can see that the Schoenfinkel combinators actually anticipated the concept of universal computing. (And even more remarkable, the definitions of S and K of 1920 are minimally simple, and resemble the very simple universal Turing machine that I proposed in the 1990s, the universality of which was proved in 2007 ).
But back to our leaflet and line PI1IIx . The characters recorded here are combinators, and they are all intended to be functions. Here the definition is that the superposition of functions should be left-associative, so fgx should not be interpreted as f @ g @ x or f @ (g @ x) or f [g [x]], but rather as (f @ g ) @x or f [g] [x]. We will translate this entry into a format convenient for use by Wolfram Language: PI1IIx will take the form p [i] [one] [i] [i] [x] .
Why write something like that? In order to explain this, we need to discuss the concept of Church numbers (named after Alonzo Church). Let's say we just work with symbols and with lambdas or combinators. Is there a way to use them to specify integers?
How about just saying that the number n corresponds to
Function[x, Nest[f,x,n]]
? Or, in other words, that (in shorter notation):
1 is
f[#]&
2 is
f[f[#]]&
3 is
f[f[f[#]]]&
and so on.
All this may seem somewhat more obscure, but the reason why it is of interest is that it allows us to do everything completely symbolic and abstract, without having to explicitly talk about something like integers.
With this method of specifying numbers, imagine, for example, adding two numbers: 3 can be represented as
f[f[f[#]]]&
and 2 is
f[f[#]]&
. You can add them simply by applying one of them to the other:
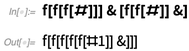
But what is f like ? It can be anything! In a sense, "go to lambda" to the end and represent numbers using functions that take f as an argument. In other words, imagine 3, for example, as
Function[f,f[f[f[#]]] &]
or
Function[f,Function[x,f[f[f[x]]]]
. (when and how you need to name variables is a catch in the lambda calculus).
Consider a fragment of Turing's 1937 paper, Computability and λ-Diffractibility , which sets up objects exactly as we just discussed:

Here, the recording may be somewhat confusing. Turing's x is our f , and his x ' (the compositor made a mistake by inserting a space) is our x . But here the exact same approach is used.
So, let's look at the line immediately after the fold in front of the leaf. This is I1IIYI1IIx . According to the form of the Wolfram Language, this will be
i[one][i][i][y][i][one][i][i][x]
. But here i is an identical function, therefore
i[one]
returns just one . Meanwhile, one is Church's numeric representation for 1 or
Function[f,f[#]&]
. But with this definition,
one[]
becomes
a[#]&
and
one[a][b]
becomes
a[b]
. (By the way,
i[][b]
, or
Identity[][b]
also a
[b]
).
It will be much clearer if we write down the replacement rules for i and one , instead of directly using the lambda calculus. The result will be the same. Apply these rules explicitly, we get:

And this is exactly the same as presented on the first abbreviated record:
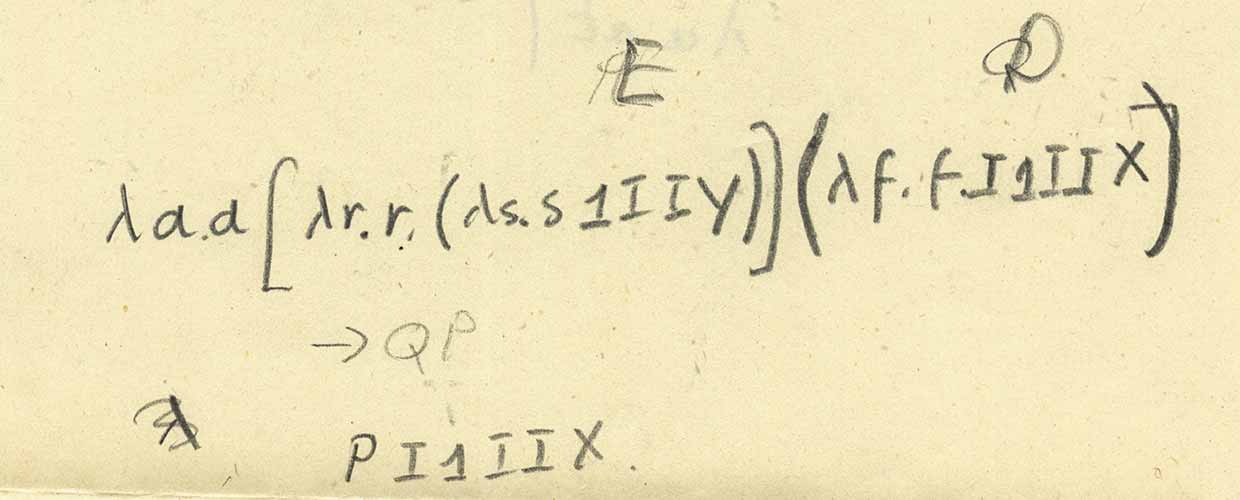
Let's now look at the leaf again, at its top:
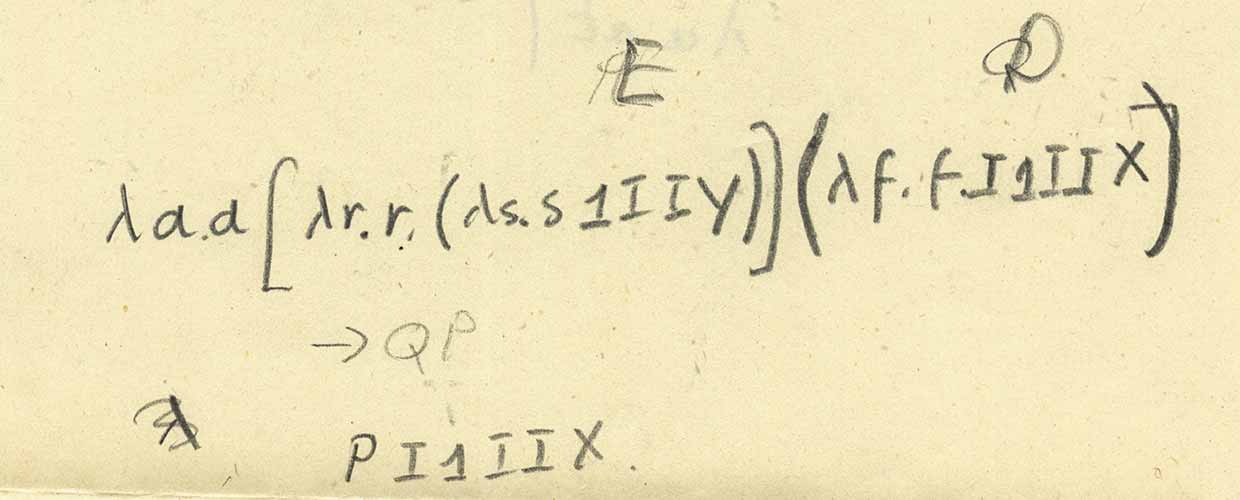
There are rather confusing and incomprehensible objects “E” and “D”, but by them we mean “P” and “Q”, so we can write out the expression and calculate it (note that here - after some confusion with the very last symbol - "mysterious scientist" puts [...] and (...) to represent the application of the function):

So this is the first abbreviation shown. To see more, let's substitute definitions for Q:

We get exactly the following abbreviation shown. What happens if we substitute the expressions for P?
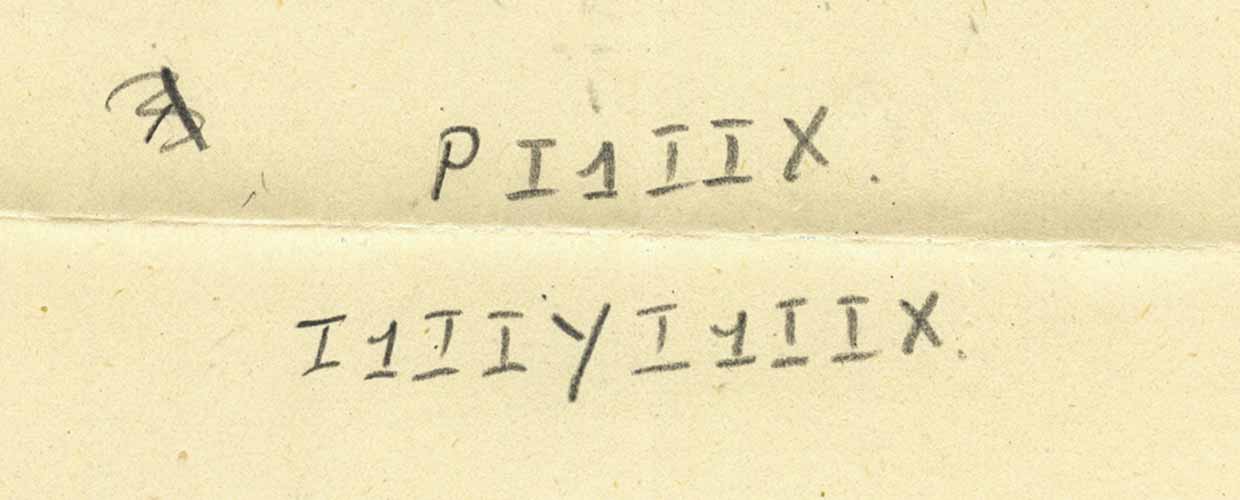
Here is the result:

And now, using the fact that i is a function that outputs the argument itself, we get:

Oooops! But this is not the next recorded line. Is there a mistake here? Unclear. Because, in the end, unlike most other cases, there is no arrow indicating that the next line follows from the previous one.
Here's some kind of mystery, but let's move on to the bottom of the leaflet:

Here 2 is the Church number, defined, for example, by the pattern
two[a_] [b_] → a[a[b]]
. Note that this is actually the form of the second line if a is treated as
Function[r,r[]]
and b as q . So, we expect the result of the calculations to be as follows:

Nevertheless, the expression
[b]
lying inside can be written as x (probably differs from x previously written on the sheet) - as a result, we get the final result:

So, we can decipher some of what is happening on this leaflet, but at least one riddle that still remains is what Y should be.
In fact, combinatorial logic has a standard Y-combinator: the so-called fixed-point combinator . Formally, it is determined by the fact that Y [ f ] must be equal to f [Y [ f ]], or, in other words, Y [ f ] does not change when f is applied, so this is a fixed point for f . (The Y combinator is associated with # 0 in the Wolfram Language.)
Currently, the Y-combinator has become famous thanks to the launch accelerator Y-Combinator , so-called Paul Graham (who for a long time was a fan of functional programming and the LISP programming language and implemented the very first web store based on this language). He once told me personally, " no one understands what Y is a combinator ." (It should be noted that Y Combinator is exactly what allows companies to avoid fixed-point operations ...)
The Y combinator (like a fixed-point combinator) was invented several times. Turing really came up with its implementation in 1937, which he called Θ. But is the letter “Y” on our page a famous fixed-point combinator? Perhaps not. So what is our “Y”? Consider this reduction:
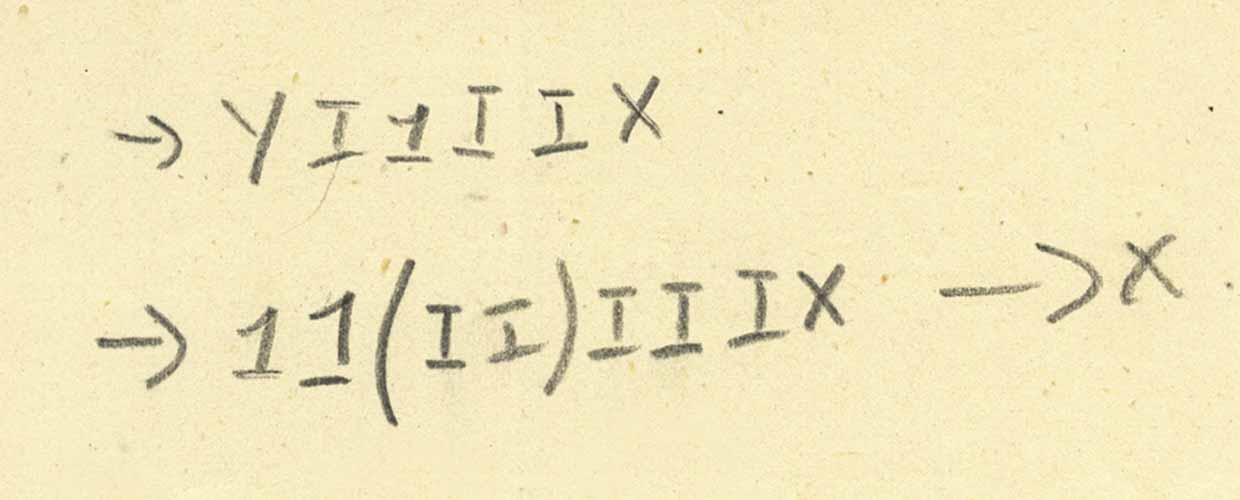
But this information is clearly not enough to unambiguously determine what Y is. It is clear that Y operates not only with one argument; it seems that the matter is at least two arguments, but it is not clear (at least to me) how many arguments it takes for input and what it does.
Finally, although we can make sense of many parts of the leaflet, we must say that on a global scale it is not clear what was done on it. Even though it requires a lot of explanations of what is presented on the sheet, it is quite elementary in lambda calculus and using combinators.
Presumably, here is an attempt to create a simple “program” - using lambda calculus and combinators in order to do something. But as far as this is typical for reverse engineering, it is difficult for us to say what this “something” should be and what a common “explainable” goal is.
There is another feature presented on the sheet, which is worth commenting here - is the use of various types of brackets. In traditional mathematics, parentheses are mainly used for everything - and applications of a function (as in f (x) ), and groupings of members (as in (1 + x) (1-x) , or, less obvious, a (1- x) ). (In Wolfram Language, we separate the various uses of brackets — in square brackets to define
f [x]
functions — and parentheses are used only for grouping).
When lambda calculus first appeared, there were a lot of questions about using brackets. Later, Alan Turing wrote a whole (unpublished) work entitled “ Transforming the mathematical form of notation and phraseology ”, but already in 1937 he felt that he needed to describe modern (rather hacker) definitions for lambda calculus (which, by the way, appeared from for Church).
He said that f applied to g should be written {f} (g) , unless f is the only character, in which case it could be f (g) . He then said that lambda (as in
Function[a, b]
) should be written as λ a [ b ] or, alternatively, λ a . b .
However, perhaps by 1940 the whole idea of using {...} and [...] to denote different objects was discarded, mainly in favor of brackets in a standard mathematical style.
Take a look at the top of the page:

In this form, it is difficult to understand. In Church definitions, square brackets are for grouping, with an opening bracket that replaces a period. Using this definition, it becomes clear that Q (eventually labeled as D), enclosed in parentheses at the end, is what the entire initial lambda applies to.
In fact, the square bracket here does not limit the body of the lambda; instead, it actually represents another application of the function, and there is no explicit indication of where the body of the lambda ends. In the end, it is clear that the “mysterious scientist” changed the closing square bracket to a round one, thereby effectively applying Church's definition - and thereby forcing to calculate the expression, as shown on the sheet.
So what does this little piece mean anyway? I think this suggests that the page was written in the 1930s, or not too long afterwards, since the legend for the brackets had not yet settled down.
So whose handwriting was it?
So, before that we talked about what is written on the page. But what about the one who wrote it all the same?
The most obvious candidate for this role would be Alan Turing himself, since, after all, the page was inside his book. In terms of content, it seems there is nothing incompatible with the fact that Alan Turing could write this - even at the moment when he first began to deal with lambda calculus after he received Church's article in early 1936.
How about handwriting? Does it belong to Alan Turing? Consider several surviving samples, which, as we know for sure, were written by Alan Turing:
The text presented clearly looks very different, but what about the notation used in the text? At least, in my opinion, this does not look so obvious - and we can assume that any difference can be caused by the fact that the existing samples (presented in the archives) are written, so to speak, “on the finish”, while ours a page is a reflection of the work of thought.
For our investigation, it turned out to be convenient that in the Turing archive there is a page on which he wrote out the symbol table necessary for the notation. And when comparing these characters letter by letter, they look pretty similar to me (these records were made at the time of Turing when he was studying plant growth , hence the notation “leaf area” appeared):

I wanted to investigate this more deeply, so I sent samples to Sheila Lowe , a professional handwriting expert (and handwriting author), whom I met once — just presenting our sheet as “sample A” and the existing Turing handwriting as "Sample" B ". Her answer was final and negative: “ The writing style is completely different. As for the personality, the author of sample “B” has a faster and more intuitive way of thinking than the author of sample “A ”. ”
I was not completely convinced of this yet, but decided that it was time to look for other options.
So if it turns out that Turing did not write this, then who did it? Norman Rutledge told me that he received the book from Robin Gandhi, who was Turing's executor. So I sent "Sample" C "" from Gandhi:

But Sheila's initial conclusion was that the three samples were probably written by three different people, again noting that sample “B” was obtained from “ the fastest thinker - the one who is most likely most willingly looking for unusual solutions to problems ” . (I find it pleasant that a modern handwriting specialist would give such an assessment of Turing's handwriting, given how actively in Turing's school assignments of the 1920s everyone complained about his handwriting).
Well, at that moment, it seemed that both Turing and Gandhi were excluded from the list of “suspects”. So who could write this? I began to think of people whom Turing could lend his book to. Of course, at the same time, they should be able to do calculations using lambda calculus.
I suggested that the person should be from Cambridge, or at least from England, given the watermark on paper. I took for the working hypothesis that 1936 or so was the right time to write this. So who did Turing know and communicate with at that time? . ( 13 , 1930 1936 .)
. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).
1937 - , , . ( , - ).
, ( ) , . ( , 1948 Turbochamp — , , ).
? LinkedIn, , , Microsoft. , , . ( ):

, ( f . .)
? , . « », , . ( , , , , , ).
— , .
«»
, . , , , , , .
, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .
? - (, , , 2005 , «»). , « ».
- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .
. , , , « ». , , , , 1954 , . , , .
, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).
, , , , , 12 , -, , , 21 ).
, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .
, , ? , , . :

, . , , , , , .
: ? , , , .
- , — 1940 — . , 1944 , , . , , .
, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)
, , . . , « » (. . -), -.
. 1969 , , , , , .
, , . . — — . . - , , .
1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).
, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .
, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .
? , , () , . ( , .) , 1 . , .
, , . : « ! » , . . , -, , , .
, , , , , . , : . ; .
, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.
, - , , , . , , , , , , . , , — , , …
: ( ), ( ) ( ).
Wolfram Language?
.
Registration for new courses . Ready online course .
Wolfram Language.