The Golden Ratio in economics - what is it?
A few words about the "golden section" in the traditional sense
It is believed that if the segment is divided into parts in such a way that the smaller part will relate to the larger, as the larger - to the whole segment, then such a division gives a ratio of 1 / 1,618, which the ancient Greeks, borrowing it from even more ancient Egyptians, called " the golden ratio. " And that many architectural structures - the ratio of the contours of buildings, the relationship between their key elements - from the Egyptian pyramids to the theoretical constructions of Le Corbusier - were based on this proportion.
She also corresponds to the Fibonacci numbers, the spiral of which gives a detailed geometric illustration of this proportion.
Moreover, the size of the human body (from the soles to the navel, from the navel to the head, from the head to the fingers of a raised hand), starting from the ideal proportions seen in the Middle Ages (the Vitruvian man, etc.), and ending with anthropometric measurements of the population of the USSR, still close to this proportion.
And if we add that such figures were found in completely dissimilar biological objects: shells of mollusks, the arrangement of seeds in a sunflower and cedar cones, then it is clear why an irrational number starting as 1,618 was declared "divine" - its traces are even traced in the form of galaxies gravitating to Fibonacci spirals!
Given all of the above examples, we can assume:
- we are dealing with truly “big data”,
- even to a first approximation, they point to a certain, if not universality, then unusually wide distribution of the "golden section" and its meanings.
In economics
Widely known and heavily used Lorentz diagrams to visualize incomes of the population. These powerful macroeconomic tools with various variations and refinements (decile coefficient, Gini index) are used in statistics for socio-economic comparison of countries and their features and can be a justification for making large political and budgetary decisions in the field of taxation, healthcare, development of country development plans and regions.
And although income and expenses are tightly connected in normal everyday consciousness, in Google it’s not so ... It’s amazing, but I managed to find the connection of Lorentz diagrams with the distribution of expenses only for two Russian authors (I would be grateful if someone knows such works as in Russian and English-speaking sector of the Internet).
The first is a thesis by T. M. Bueva. The thesis was devoted, in particular, to cost optimization at Mari poultry farms.
Another author, V.V. Matokhin (reciprocal links of authors are available), approaches the matter on a larger scale. Matokhin, a physicist in primary education, is engaged in the statistical processing of data used in making managerial decisions, as well as in assessing the adaptability and manageability of companies.
The concept and examples given below are drawn from the work of V. Matokhin and his colleagues (Matokhin, 1995), (Antoniou et al., 2002), (Kryanev et al., 1998), (Matokhin et al. 2018). In this regard, it should be added that possible errors in the interpretation of their works are the exclusive property of the author of these lines and cannot be attributed to the original academic texts.
Unexpected constancy
Reflected in the graphs below.
1. Distribution of grants for the competition of scientific and technical works under the State program “High-Temperature Superconductivity”. (Matokhin, 1995)
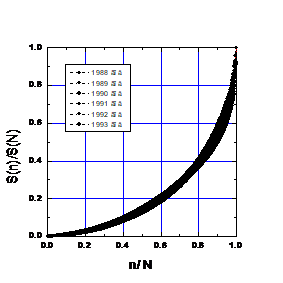
Fig. 1. Proportions in the annual allocation of funds for projects in 1988-1994.
The main characteristics of the annual distributions are shown in Table 3, where SN is the annual amount of allocated funds (in million rubles), and N is the number of funded projects. Given the fact that the composition of the jury, the budget of the competition, and even the scale of money (before the 1991 reform and after) have changed over the years, the stability of real time curves is amazing. The black bar on the graph is made up of experimental points.
| 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | ||
| S | 273 | 362 | 432 | 553 | 345 | 353 | 253 | X |
| Sn | 143.1 | 137.6 | 136.9 | 411.2 | 109.4 | 920 | 977 | Y |
Table 3
2. The curve of costs associated with sales of inventory (Kotlyar, 1989)

Fig.2
3. Chin salary rate schedule
As an example, for constructing the diagram, we took the data from the document “Bulletin: how many ranks according to the states of the ordinary annual salary per year should have” (Suvorov, 2014) (“The Science of Winning”).
| 
Fig. 3. The proportionality chart of annual salaries by rank |
4. The average work schedule of the American mid-level manager (Mintzberg, 1973)

Fig. 4
The normalized graphs given suggest that there is a general pattern in the economic activities they illustrate. With a radical difference in the specifics of economic activity, in its place and time, it is very likely that the similarity of the schedules is dictated by some fundamental condition for the functioning of economic systems. In the course of millennia of conducting economic activity, on the basis of a huge number of trial and error, the subjects of this activity have groped for some optimal resource allocation strategy. And intuitively use it in current activities. This assumption is in good agreement with the well-known Pareto principle: 20% of our efforts yield 80% of the results. Something similar is clearly observed here. The given graphs express an empirical regularity, which, when converted to a Lorenz diagram, is described with sufficient accuracy when the exponent "alpha" is equal to 2. In this indicator, the Lorentz diagram turns into part of a circle.
You can call this, not yet having a stable name characteristic, survival. By analogy with survival in the wild, the survival of an economic system is determined by its proven adaptation to the conditions of the socio-economic environment and its ability to adapt to changes in market conditions.
This means that a system in which the distribution of expenditures is close to ideal (with a degree of alpha equal to 2, or the distribution of expenditures "around the circumference") has the greatest chance of being maintained in its existing form. It is noteworthy that in some cases, such a distribution determines the highest profitability of the enterprise. For example, here. The lower the coefficient of deviation from the ideal, the higher the profitability of the enterprise (Bueva, 2002).
Table (fragment)
| Name of farm, district | Profitability (%) | Deviation coefficient | |
| one | State Unitary Enterprise p / f "Volzhskaya" Volzhsky district | 13.0 | 0.336 |
| 2 | SPK p / f "Gornomariyskaya" | 11.1 | 0.18 |
| 3 | UMSP sz Zvenigovsky | 33.7 | 0,068 |
| four | CJSC Mariyskoye, Medvedevsky District | 7.5 | 0.195 |
| five | OJSC "Teplichnoe" of the Medvedevsky district | 16.3 | 0.107 |
| ... | |||
| 47 | SEC (KZ) "Dawn" of the Soviet district | 3.2 | 0,303 |
| 48 | C-s “Armored Car” of the Kilemarsky district | 14.2 | 0.117 |
| 49 | SPK SCA "Vanguard" of the Morkinsky district | 6.5 | 0.261 |
| 50 | SHA to them. Petrov Morkinsky district | 22.5 | 0.135 |
Practical findings
When planning expenses for both a company and a household, it is useful to construct the Lorentz curve from them and compare it with the ideal one. The closer your chart is to ideal, the more likely it is that you are planning correctly and that your activity will be successful. Such closeness confirms that your plans are close to the experience of the economic activities of mankind, deposited in such universally recognized empirical laws as the Pareto principle.
However, we can assume that here we are talking about the functioning of a mature economic system focused on profitability. If we are not talking about maximizing profits, but, for example, about the task of modernizing the company or about fundamentally increasing its market share, your curve of the distribution of costs will depart from the circle.
It is clear that in the case of a start-up with its specific economy, the Lorentz diagram corresponding to the highest probability of success will also deviate from the circle. It can be hypothesized that deviations of the distribution curve of expenses within the circle correspond to both increased risks and reduced company adaptability. However, without reliance on large statistical arrays for start-ups (both successful and unsuccessful), reasonable qualified forecasts are hardly possible.
According to another hypothesis, the deviation of the curve of the distribution of costs from the circle to the outside, can be a signal as an excessive regulation of control, and a signal of impending bankruptcy. To test this hypothesis, a certain reference base is also necessary, which, as in the case of start-ups, is unlikely to exist in the public domain.
Instead of a conclusion
The first large publications on this subject date back to 1995 (Matokhin, 1995). And the little-known of these works, given their universality and the radically new use of models and tools widely used by economists, remains in a sense a mystery ...
All Articles