The universe did not start with the Big Bang, but with the Big Melting

Cosmological constant and the creation of the universe

Regarding the Universe, there are two particularly painful unsolved riddles, one of which is connected with its ultimate fate, and the second with the beginning, intriguing cosmologists for decades. The academic community has always believed that these two tasks are independent of each other - but what if it is not so?



The first task is connected with the existence of something called “dark energy”, which today is accelerating the expansion of the Universe, and as a result will determine its final fate. Theorists say that the action of dark energy can be explained by introducing into the Einstein's equations a new term called the “cosmological constant”. But for this explanation to work, the cosmological constant must have a definite, very small value. In natural units, it is defined by a unit divided by a number consisting of 123 characters! The explanation of the value of this constant is one of the most difficult problems of theoretical physics.





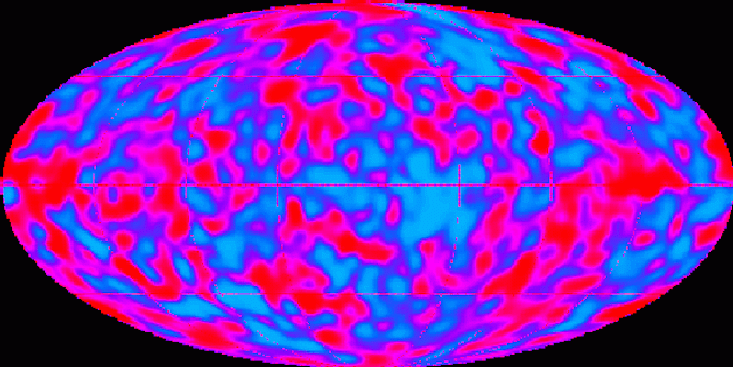
Variations of the CMB indicate fluctuations in the density of the early Universe.



The second problem is connected with another important number defining our Universe and with the formation of such structures as galaxies and groups of galaxies. We know that the early Universe, although it was very homogeneous, contained small fluctuations in density, which became the root causes of the cosmic structures that we see today. To coincide with our observations, these fluctuations had to have a certain size and shape. The way these fluctuations appeared in the earliest periods of the evolution of the Universe, and their shape and size are equally amazing mysteries of cosmology.



With the generally accepted approach to cosmology, these two numbers — the value of the cosmological constant and the value of the initial perturbations — are not considered to be related. Indeed, one of them deals with the earliest phase of the Universe, and the second with the latest, and they are separated by cosmic time of 14 billion years. Moreover, standard cosmology does not explain these values ​​on the basis of fundamental principles. The generally accepted models of the Universe say nothing about the numerical value of the cosmological constant, or predict completely different values. Regarding the magnitude of the initial disturbances, the most popular approach is to obtain this value from the class of models describing inflation - a period of rapid growth in the early phase of the Universe. The problem with inflationary models is that they can be tailored to produce almost any result, which is why they have no predictive ability.



In my recent work, carried out with my daughter, Hamsa Padmanabhan and Tomalla Fellow at the Swiss Technical School Zurich, both of these numbers are associated with cosmogenesis - the creation of the Universe - and their exact meaning is explained. Our work, recently published in Physics Letters B, shows that the very existence of a cosmological constant, like its tiny value, can be represented as a direct consequence of the information content of cosmic spacetime [Padmanabhan, T. & Padmanabhan, H. Cosmic information, the cosmological constant and the amplitude of primordial perturbations. Physics Letters B 773, 81-85 (2017)]. In addition, the analysis gives the correct value of the size and shape of small fluctuations of the early Universe.



The remarkable relationship of these fundamental constants is important for our understanding of the Universe. In particular, it changes our understanding of the Big Bang and eliminates the need for a period of inflation at an early stage of the Universe.



The Big Bang is probably the most famous feature of standard cosmology. But he is also not very necessary for her. The classical model of the Universe, described by Einstein's equations, ceases to work under the conditions of the Big Bang, with infinite density and temperature — this is the situation that physicists call a singularity.



But what if there was no singularity? Since the 1960s, physicists have been working on the description of the universe without the Big Bang, trying to combine the theory of gravity and quantum theory into something called “quantum gravity”. Physicists John Wheeler and Bryce Devitt were the first to apply these ideas to the hypothetical pre-geometric phase of the Universe, in which the concepts of space and time have not yet emerged from an unknown structure. This led to the emergence of quantum cosmology, in which physicists are trying to describe the dynamics of simple, toy models of the universe in a quantum language. Needless to say, over the decades, several different, though related to each other, ideas of describing the pre-geometric phase suddenly appeared. What unites them is that the classical Universe without any singularity appears through a series of transformations from the pre-geometric phase to the one in which space-time is described by the Einstein equations. The main difficulty in constructing such a description is that we do not have a complete theory of quantum gravity, which would allow us to model the pre-geometric phase in detail.





Einstein several times called his addiction to the cosmological constant in his equations a gross error. Today, physicists believe that it has a positive meaning.



The key ingredient we have introduced to help circumvent this technical complexity is the concept of space information. Recently, the idea that information should play a key role in describing physics is gaining more and more support. It appears in several cases where scientists are trying to combine the principles of quantum theory and gravity - for example, when studying quantum black holes. Also in some of these models there is an intriguing idea of ​​holography, which states that the content of a voluminous region may be related to the information content of its borders. But, unfortunately, the mathematical description of information in different cases turns out to be different, and the unifying principle, applicable in all cases, has not yet been found. Therefore, in order to apply the idea of ​​information to the entire Universe, we first had to come up with a physically appropriate definition for it.



The definition of space information we use can be described using an analogy. When a piece of ice melts and turns into water, a phase transition from a solid to a liquid state occurs. Real phase transition processes can be extremely complex, but the total number of ice atoms will be the same as the number of water atoms. This number determines the number of degrees of freedom of the system, not changing during the phase transition. Similarly, the phase transition that led to the appearance of the Universe can be described by a number connecting the number of degrees of freedom in the pre-geometric phase with the number inherent in the classical space-time. Using this number, which we called the cosmin [CosmIn], we can combine the two phases of the Universe, and circumvent the complexity of the complete model of quantum gravity.



Cosmin, as a physically observable number, must be finite. In the absence of singularities, we believe that all physical quantities must be finite. In addition, we were able to show that the cosmin will be finite only if the Universe experiences an accelerated expansion phase in the late period of its existence, the way we see it today. This connection not only indicates the existence of a fundamental reason for the existence of a cosmological constant, but also about how to calculate its numerical value - if we know the value of the cosmin.



The value of the cosmin in the pre-geometric or quantum-gravitational phase of the Universe can be determined using the results that periodically appear in different models of quantum gravity. It turns out that the total amount of information transmitted from the quantum-gravitational phase to the classical phase should be equal to a simple number: 4π, the area of ​​a sphere of a single radius. Using this fact, we can associate the numerical value of the cosmological constant with the energy scale at which the Universe passed from the quantum-gravitational phase to the classical one.



This energy transition scale can be associated with the second mysterious property of our Universe: the size of tiny quantum fluctuations in the early Universe, which grew and formed galaxies and galactic clusters that we see today. A popular system for calculating the size of these fluctuations uses inflationary models of the Universe, which describe the Universe passing through an incredible large and rapid expansion in size. But there are a lot of inflationary patterns and they are very different, and they can give any desired value. It is also worth noting that the form of the original fluctuations was obtained by Edward Robert Harrison in 1970 (and independently of him by Yakov Zeldovich), and is called the Harrison-Zeldovich spectrum. But people forget to point out that Harrison got his result more than ten years earlier before the invention of inflation models!



Our model allows us to relate both quantities — the magnitude of the cosmological constant and the size of the initial fluctuations — to the scale of energy on which the pre-geometric Universe experienced a phase transition and became the classical Universe in which we live. And, attention, when we select the right energy scale, we get the correct, observable value for both of these values. This leads us to the algebraic relationship between the cosmological constant, the magnitude of the original fluctuations and the cosmic one. We can reverse this relationship using the observed cosmological parameters, and check whether the value of the cosmin is 4π. The theory is well tested; we find that the cosmin, determined from observations, is 4π with an accuracy of 1/1000.



Surprisingly, a complex combination of cosmological parameters that were considered unrelated to each other has such a simple meaning. A common approach would be to consider such a connection as random coincidence. We believe that she tells us something deep and beautiful about our Universe.



We believe that we made the first attempt to associate the numerical value of the cosmological constant with the size of fluctuations in the early Universe, and obtain both of these values ​​from a model that does not have adjustable parameters and connects them with the energy scale on which the Universe began to exist.



All these ideas exist on a more general platform of quantum gravity, a theory that physicists, despite almost five decades of development, still do not have. One of the advantages of our model is that it does not need the details of quantum gravity. But it makes two important clues about the nature of quantum gravity and the structure of spacetime. First, it says that space-time must be represented consisting of microscopic degrees of freedom, just like matter consisting of atoms. Secondly, she argues that the correct theory of the origin of the Universe should include a phase transition from the pre-geometric phase to the classical phase.



These clues can answer the key question: why, after several decades of work, theorists have not combined gravity and quantum theory? We believe that this is best explained by another analogy. We know that fluid dynamics is a consistent physical theory, expressed through a set of equations. If we take them as fundamental and apply the principles of quantum theory to them, we can discover a new interesting phenomenon — for example, phonons (vibration quanta) and their interactions. However, using this approach, we can not get to the quantum structure of matter.



There is evidence that the equations describing gravity in this sense are similar to the dynamics of liquids. In other words, the reformulation of equations describing gravity, using the principles of quantum theory, is similar to the application of quantum principles to the equations of fluid dynamics. We will not open the quantum structure of space-time in this way - and we believe that because of this decade, attempts to quantify Einstein's theory ended in a loud failure.



Instead, we need to rethink the nature of gravity and understand what it tells us about the microscopic structure of spacetime. Such an approach was used by physicist Ludwig Boltzmann to understand that temperature phenomena require the notion of matter as consisting of discrete degrees of freedom (in other words, atoms). Boltzmann, in fact, said that if something could be hot, it should contain microscopic degrees of freedom.



Spacetime can also have temperature and appear hot to certain observers. This idea came about through the work of Jacob Beckenstein and Stephen Hawking in the context of black holes. Shortly thereafter, in the mid-70s, the works of Bill Unrich and Paul Davis showed that this is a basic property of spacetime. Combining the Boltzmann paradigm with the fact that space-time - like ordinary matter - can be hot, you will come to the conclusion that space-time should have internal degrees of freedom, like atoms in matter. Theoretical evidence in support of this conclusion has begun to emerge in recent years [Padmanabhan, T. The atoms of spacetime and the cosmological constant. Journal of Physics: Conference Series 880, 012008 (2017)]. This observation contains the key to understanding the microstructure of space-time, which quickly leads to remarkable results.



First, the evolution of a portion of space-time can be described in terms of the degrees of freedom (or, equivalently, of the information content) located within the boundaries of this portion. Secondly, gravity becomes insensitive to changes at zero energy level. In Einstein's theory, gravity is responsible for the absolute amount of energy, because of which the cosmological constant is almost impossible to calculate. But for the paradigm based on the informational content, this is not the case. Thirdly, the informational approach suggests that we should not imagine the cosmic evolution according to a certain solution of the Einstein equations. These equations arise from a more accurate set of equations describing the quantum degrees of freedom of spacetime [Padmanabhan, T. Do We Really Understand the Cosmos? Comptes Rendus Physique 18, 275-291 (2017)].



Informational approach, confirmed by our model of cosmin, gives us a new, vivid picture of the Universe, similar to a large piece of ice containing a source of heat. The heat source melts the ice around it, creating a plot of water that expands, reaching local thermodynamic equilibrium. On a large scale, closer to the phase boundary, the molecules have not yet reached equilibrium, since a piece of ice heats up from the inside. Interestingly, this is very similar to the behavior of our universe. The area with water is similar to the observable Universe (as described by Einstein's theory). It is surrounded by a dogometric phase (similar to ice), described by the laws of quantum gravity that are not yet known. The idea of ​​the Big Bang disappears, and a transition from one phase to another along their border appears instead. Also eliminates the need for an inflation period.



The whole platform is simple and elegant, since it is described by a single parameter: the energy scale of the phase transition of the early Universe from pre-geometry to Einstein geometry. This is different from ordinary inflationary models that contain many parameters and do not have predictive capabilities. Our model does not use unverified physics. The only postulate we have made is that the content of the Universe should be 4π, the surface area of ​​a single sphere.



The work opens up three new areas of research. First, she invites us to study the physics of the pre-geometric phase in various models of quantum gravity. Second, it opens up the possibility to study the idea of ​​cosmic information used in this work and try to connect it with other similar ideas used in other contexts. Third, it reinforces the idea that space-time consists of more elementary degrees of freedom — just like matter consists of atoms — and encourages us to study different phases of space-time as we study different phases of matter in condensed matter physics .



Tanu Padmanabhan is a professor at the Interuniversity Center for Astronomy and Astrophysics of India.